Today, I will talk about discovering interesting patterns in data, what is called pattern mining, and in particular about how the concept of taxonomy can be useful to find interesting patterns. There has been a lot of research on pattern mining over the years to find various types of interesting patterns in data, and numerous algorithms have been designed for that. To explain the interest for taxonomies in finding patterns, I will talk about a classical problem in pattern mining called high utility itemset mining.
High Utility Itemset Mining
High utility Itemset mining aims at searching in data to find itemsets (sets of values) that have a high importance as measured by a utility function. There are many applications of this problem, but let me illustrate it with shopping data as it is a popular example.
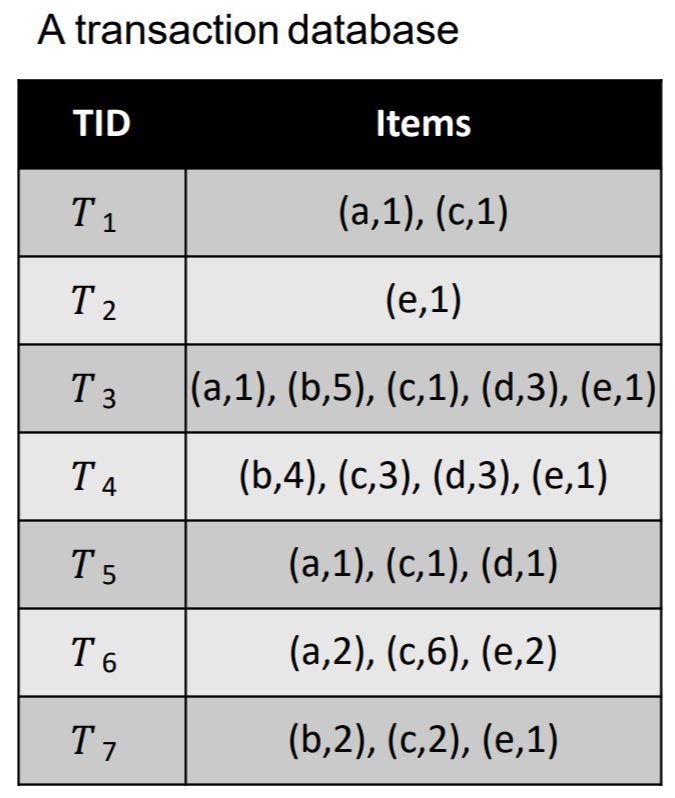
The input of high utility Itemset mining in that context is a database containing a set of records called transactions. Each transaction indicates the items (products) that some customer has purchased at some moment. For example, let’s look at this database of seven transactions, called T1, T2 .. T7:
The first transaction (called T1) indicates that a customer purchased two products (items) called “a” and “c”, which could represent for example the products “apple” and “cake”. The number 1 besides “a” and the number 1 besides “c” indicate that the customer purchased 1 unit of item “a”, and 1 unit of item “c”, that is one apple and one cake. The second transaction (called T2) indicates that a customer purchased 1 unit of item “e”, which could stand for “egg”. The sixth transaction (T6) indicates that a customer purchased 2 apples, 6 cakes and 2 eggs.
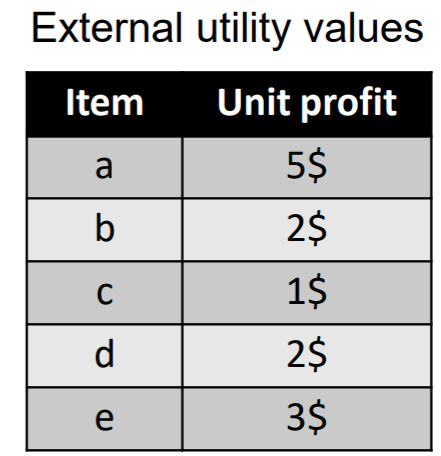
Furthermore, another table shown below indicates the utility (relative importance) of each item, which in this case is the unit profit (how much money a store earns by selling one unit of an item).
This table indicates for example that selling 1 unit of item “a” yields a 5$ profit, while selling 1 unit of item “b” yields a 2$ profit, and so on.
Having such data, it is possible to calculate how much utility (money) is obtained from the sale of different Itemsets (sets of products). For example, consider the itemset {b,c,d}. The utility of that itemset is the amount of money obtained when “b”, “c” and “d” are sold together. This is calculated as follows. First, we observe that “b,c,d” are purchased together in two transactions (T3 and T4), highlighted in red color below:
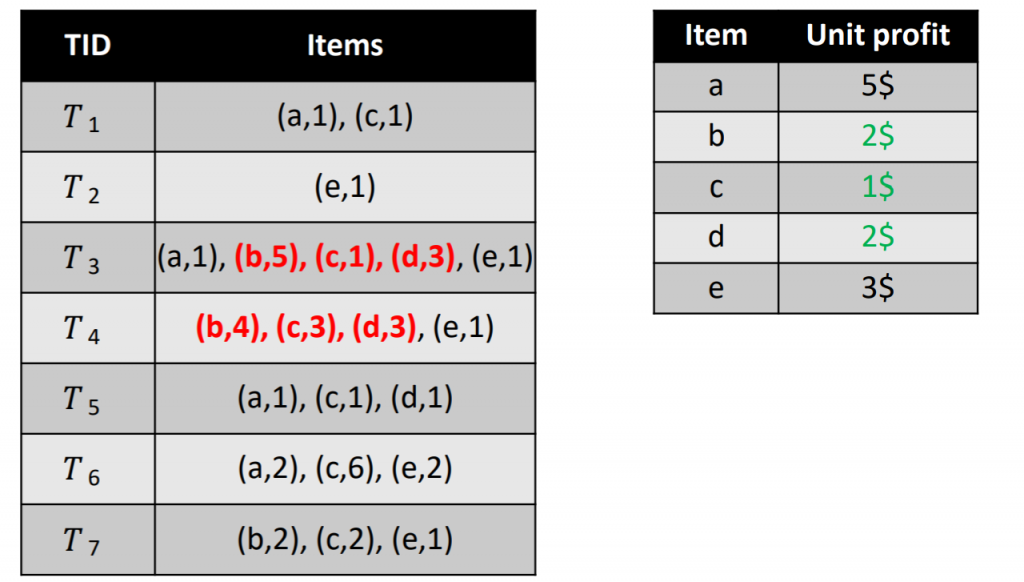
To find the amount of money (utility) that {b,c,d} yields in transaction T3, we multiply the number of units of each item by its unit profit, as follows. Since, there are 5 units of item “b” and its unit profit is 2, there is 1 unit of item “c” and its unit profit is 1, and there are 3 units of item “d” and the unit profit of “d” is 3, the calculation is: (5 x 2) + (1 x 1) + (3 x 2) = 17.
To find the amount of money (utility) that {b,c,d} yields in T4, we multiply the number of units of each item by its unit profit, as follows. Since, there are 4 units of item “b” and its unit profit is 2, there is 3 unit of item “c” and its unit profit is 1, and there are 3 units of item “d” and its unit profit is 3, the calculation is: (4 x 2) + (3 x 1) + (3 x 2) = 17.
Then, we do the sum of the utility of {b,c,d} in transactions T3 and T4 to find its total utility, which is 17 + 17 = 34.
The problem of high utility itemset mining applied to such data consists of finding the itemsets (sets of products) purchased together that yield a profit that is no less than a threshold called minutil. For instance, if minutil = 30$, then there are 8 such itemsets, which we call the high utility itemsets. They are:

where each itemset is annotated with its utility (profit). For instance, as can be seen above, {b,c,d} is a high utility itemset as it yield 34$, which is no less than minutil = 30$.
There exists several algorithms to quickly find all high utility itemsets in a dataset such as FHM, EFIM, HUI-Miner, ULB-Miner and UP-Growth.
Finding high utility itemsets can be useful to reveal patterns in the shopping habits of customers, and can be also applied to other fields where the concept of “utility” may have other meaning than the money. However, a major limitation of high utility itemset mining is that there is no concept of categories of items. But in real life, items in stores are generally categorized or grouped. For example, various milk bottles of different sizes and brands can all be viewed as belonging to a category milk. Similarly, all types of cheese, yogurt and milk can be viewed as members of a higher level category called dairy products. In many cases, when analyzing data, it is preferable to view items of a same category together rather than evaluating them individually. For instance, it may make more sense in some contexts to just talk about chocolate in general than each different brands of chocolate bars.
Multi-level high utility Itemset mining
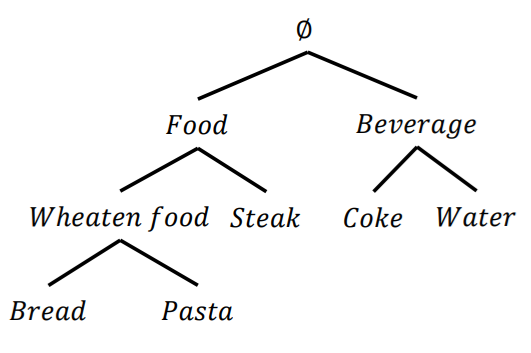
To be able to consider product categories in high utility Itemset mining, Cagliero et al (2017) proposed the task of multi level high utility Itemset mining. In this problem, a taxonomy must be provided by the user, indicating the categories of products. A taxonomy is like a tree where each category can be divided in sub categories, and nodes at the bottom of the tree (the leaves) contain the items. For example, a taxonomy is shown below:
This taxonomy contains several levels. A the bottom level (the leaves), the items “coke”, “water”, “bread” and “pasta” are found. At the second level, these items are grouped into categories called “Weaten food” and “Beverage”. At the third level, there is a category called “Food” and finally, the root of the tree is the category containing everything.
Clagliero et al. proposed an algorithm called MLHUI-Miner to finds high utility itemsets at different levels of a taxonomy. This can allow to find high utility itemsets containing categories instead of items. For example, using the above taxonomy, MLHUI-Miner could find a high utility itemset such as:
{Wheaten food, Beverage}
where Wheaten food and Beverage are categories grouping several products. However, a major limitation of the problem defined by Clagliero et al is that a same itemset is not allowed to contain categories from different levels. This means that itemsets such as {Bread, Beverage} cannot be found because “bread” and “beverage” do not belong to the same taxonomy level. Thus, several interesting patterns may be missed by MLHHUI-Miner.
Cross-level high utility Itemset mining
To address the above problem, Fournier-Viger et al. (myself) proposed the more general problem of cross-level high utility itemset mining. The goal is to find high utility itemsets where items and categories can be mixed from any taxonomy level. I will give a brief explanation of this problem with an example. Consider the same database that I have shown before, but this time there is a taxonomy that is provided, shown on the right:
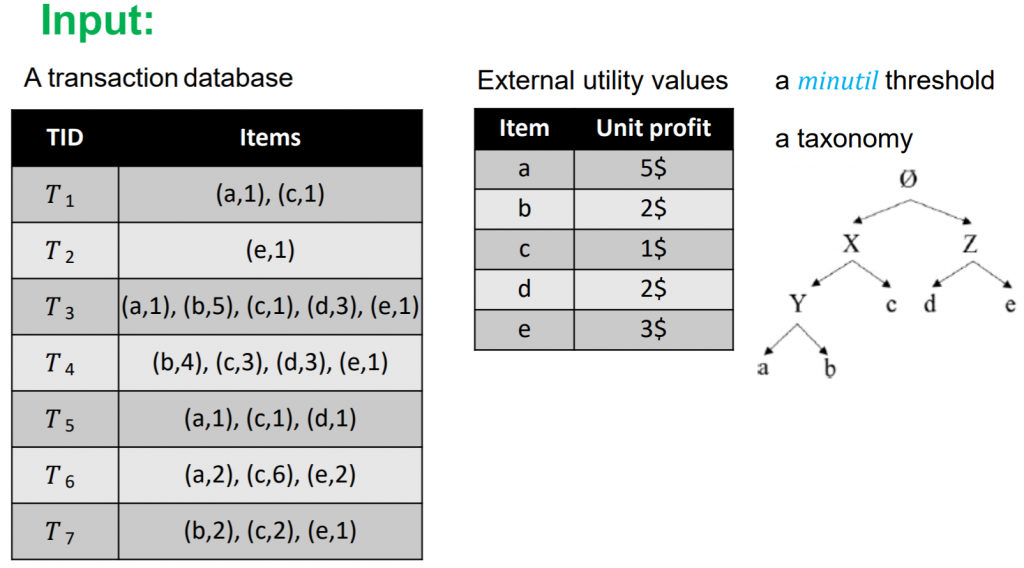
This taxonomy indicates that a category X contains an item “c” and a sub-category “Y” of “X” contains two items “a” and “b”. Furthermore, a category “Z” contains two items “d” and “e”.
Using such taxonomy, it is possible to calculate the utility of itemsets containing items and/or categories. To explain this, I will give an example of calculating the utility for the itemset {Y,C}, which means the total amount of money for all transactions that contain “a” and/or “b” with item “c”. To calculate this, we first observe that itemset {Y,c} appears in transactions T1, T3, T4, T5, T6 and T7. Thus, we calculate the utility of {Y,c} in these transactions and do the sum:
In Transaction 1, we multiply 1 unit of item “a” by its unit profit of 5$, and add 1 unit of item “c” multiplied by its unit profit of 5$, thus: (1 x 5 + 1 x 1)
In Transaction 2, we multiply 1 unit of item “a” by its unit profit of 5$, add 1 unit of item “b” multiplied by its unit profit of 2$, and add 1 unit of item “c” multiplied by its unit profit of 1$ thus: (1 x 5 + 5 x 2 + 1 x 1)
…
and we do this also for the transactions T4, T5, T6 and T7.
This gives us the following sum for the transactions T1, T3, T4, T5, T6 and T7:
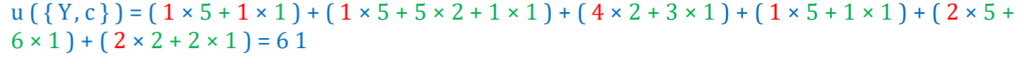
which indicates that the total utility of {Y,c} is 61$.
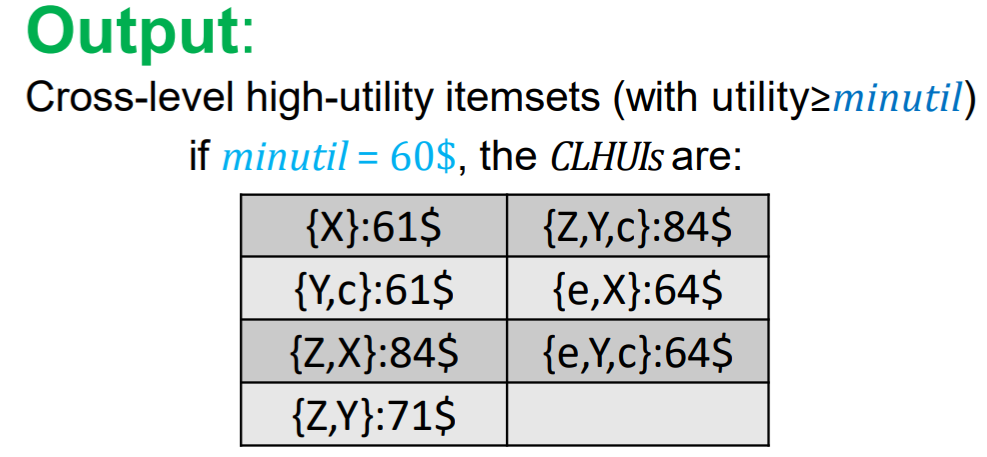
In cross-level high utility itemset mining, the user must set a minutil threshold. If we set this threshold to 60$, then the goal is to find all the cross-level high utility itemsets, that is the itemsets that yield a profit of at least 60$ and contain items or categories. For example, for the above example, the result is:
In this example, there are several itemsets like {Y,c} that are contain items/categories from different taxonomy levels. Those cannot be found by MLHUI-Miner.
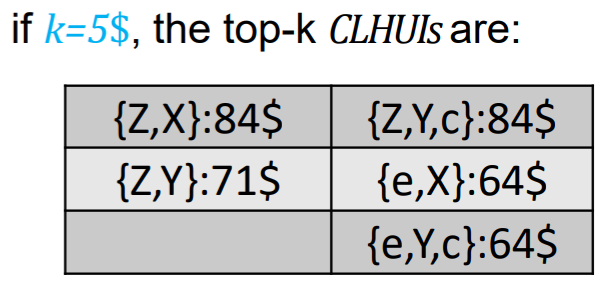
The CLH-Miner algorithm is the first algorithm to be proposed for this new generalized problem of cross-level high utility itemset mining. Then, another algorithm called TKC was proposed for a variation of this problem called finding the top-k cross-level high utility itemsets. In that problem, rather than using minutil, the user must set a parameter k and TKC will output the k cross-level itemsets that have the highest utility. For example, if we set k = 5, TKC will produce this result:
TKC is an interesting algorithm because setting the parameter “k” is usually more intuitive for the user than using the “minutil” parameter. For example, using TKC, a retail store owner can directly look for the top 5 itemsets that yield the most profit. But using the “minutil” threshold, it is not obvious to know how many patterns will be found before running the algorithm.
Finding cross-level high utility itemsets in real shopping data
If you want to try high utility Itemset mining with a taxonomy, the source code of CLH-Miner, TKC and MLHUI-Miner can be obtained as part of the open source SPMF data mining library.
There are also some real transaction datasets with taxonomies called Liquor and Fruithut, that you can download from the SPMF website’s dataset page. Liquor contains 9,284 transactions from liquor stores in the US, where there are 2,626 items and the taxonomy contains 7 levels. Fruithut contains 181,970 transactions from fruit stores in the US, where there is a taxonomy of 4 levels.
By applying the CLH-Miner or TKC algorithm, several interesting patterns can be found. For example, in the Fruithut dataset, the itemset {bean, cherries} is found, which indicates that people like to purchase beans with cherries and that it is profitable. In that itemset, “beans” is a category. Here is a part of the taxonomy from Fruithut that shows the different kinds of beans under that category:
Another example of real cross-level high utility itemsets is the following. In the Liquor dataset the itemset {Cordials& Liqueurs, Neutral Grain Spirits} indicates that customers purchase “cordials and liqueurs” with “neutral grain spirits” and this yield a lot of money in Liquor stores.
References on this topic
If you want to know more about this topic, the algorithms that I have discussed in this blog post are described in a more formal way in these papers:
- TKC : Nouioua, M., Wang, Y., Fournier-Viger, P., Lin, J.-C., Wu, J. M.-T. (2020). TKC: Mining Top-K Cross-Level High Utility Itemsets. Proc. 3rd International Workshop on Utility-Driven Mining (UDML 2020), in conjunction with the ICDM 2020 conference, IEEE ICDM workshop proceedings, to appear. [ppt]
- CLH-MINER: Fournier-Viger, P., Yang, Y., Lin, J. C.-W., Luna, J. M., Ventura, S. (2020). Mining Cross-Level High Utility Itemsets. Proc. 33rd Intern. Conf. on Industrial, Engineering and Other Applications of Applied Intelligent Systems (IEA AIE 2020), Springer LNAI, pp. 858-871. [source code][ppt]
- MLHUI-MINER:. Cagliero, T. Cerquitelli, P. Garza, and L. Grimaudo, “Misleading generalized itemset discovery,” Expert Syst. Appl., vol. 41, pp. 1400– 1410, 2014.
Besides, if you are interested by an overview of high utility itemset mining, I have written an easy-to understand survey:
- Fournier-Viger., P., Lin, J. C.-W., Truong, T., Nkambou, R. (2019). A survey of high utility itemset mining. In: Fournier-Viger et al. (eds). High-Utility Pattern Mining: Theory, Algorithms and Applications, Springer (to appear), p. 1-46.
Conclusion
In this blog post, I have discussed the problem of high utility itemset mining with a taxonomy to give an introduction to this topic. The studies in this blog post were inspired by early work on frequent itemset mining with a taxonomy. Besides, it is to be noted that taxonomy can be used or has been used in other pattern mining problems such as sequential pattern mining, episode mining and periodic pattern mining. For researchers, there are also many opportunities to extend the algorithms like CLH-Miner and TKC that I have presented above.
If you have comments, please share them in the comment section below. I will be happy to read them.
—
Philippe Fournier-Viger is a full professor and founder of the SPMF open source data mining software.