An Introduction to High Utility Quantitative Itemset Mining

Today, I will talk about pattern mining, a subfield of data science that aims at finding interesting patterns in data. More precisely, I will briefly describe a popular data mining task named high utility itemset mining. Then, I will describe a limitation of this task, which is the lack of information about quantities in the discovered patterns, and an extension that address this issue, called high utility quantitative itemset mining.

High Utility Itemset Mining

High utility itemset mining is a data mining task, which consists of finding patterns that have a high utility (importance) in a dataset, where the utility is measured using a function. There are various applications of this task, but the most representative one is to analyze customer transactions to find sets of products that people like to purchase together and yield a high profit. I will thus briefly explain what is high utility itemset mining for this application. In that context, the input is a transaction dataset, as illustrated in the table, below.

This dataset contains seven records called T1, T2, T3, T4, T5, T6, T7. Each record is a transaction, indicating what items (products) a customer has purchased in a store at a given time. In this example, the products are called “a”, “b”, “c”, “d” and “e”, which stands for apple, bread, cake, dattes and eggs. The first transaction (T1) indicates that a customer has purchased one unit of item “a” (one apple), with one unit of item “c” (one cake). The sixth transaction (T6) indicates that a customer has bought two units of “a” (two apples) with 6 units of “c” (six cakes) and 2 units of “e” (two eggs). Other transactions follow the same format.

Moreover, another table is taken as input, shown below, which indicates the amount of money that is obtained by the sale of each item (the unit profit).

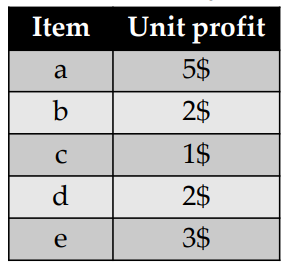
For instance, in that table, it is indicated that selling an apple (item “a”) yields a 5$ profit, while each bread sold (item “b”) yields a 2$ profit.

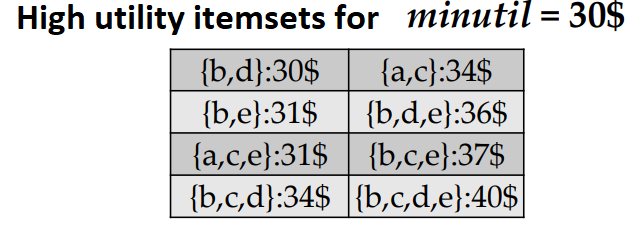
The goal of high utility itemset mining is to find the itemsets (sets of items) that yield a utility (profit) that is greater than or equal to a threshold called the minimum utility (minutil) threshold, set by the user. For instance, if the user sets minutil = 30$, the goal is to find all the sets of items (itemsets) that yield at least 30$ in the above database. Those itemsets are called the high utility itemsets. For this example, there are only 8 high utility itemsets, which are shown below with their utility (profit) in the database.

For instance, the itemset {b,c,d} has a utility of 34$, and it is a high utility itemset because 34$ > minutil = 30 $. But how do we calculate the utility (profit) of an itemset? Let me explain this more clearly.

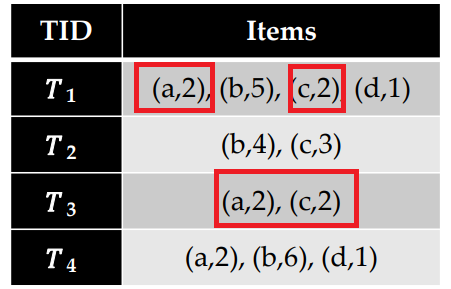
Let’s take the itemset {b,c,d} as example. To calculate the utility (profit) of {b,c,d}, we first need to find all the transactions that contain {b,c,d} together. There are only two transactions (T3 and T4), highlighted below:

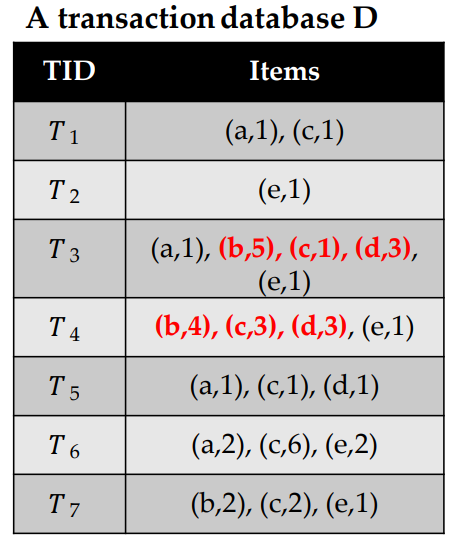
After we have found that, we need to calculate the utility of {b,c,d} in transaction T3 and in transaction T4 and do the sum.

Let’s first look at T3. Here, we have 5 units of “b” which have a unit profit of 2$ with 1 unit of item “c” that has a unit profit of 1$, and 3 units of “d” which has a unit profit of 2$. Thus, the utility of {b,c,d} in T3 is (5 x 2 ) + (1 x 1) + ( 3 x 2) = 17 $.

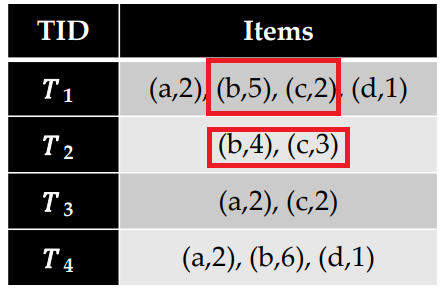
Now, lets look at T4. Here, we have 4 units of “b” which have a unit profit of 2$ with 3 unit of item “c” that has a unit profit of 1$, and 3 units of “d” which has a unit profit of 2$. Thus, the utility of {b,c,d} in T3 is (4 x 2 ) + (3 x 1) + ( 3 x 2) = 17 $.

Then, we do the sum of the utility of {b,c,d} in T3 and T4 to get its total utility (profit) in the whole database, which is 17$ + 17 $= 34 $.

To find the high utility itemsets in a database, many algorithms have been designed such as FHM, EFIM, HUI-Miner, ULB-Miner and UP-Growth. I have published a good survey on high utility itemset mining, which gives more details about it.

High Utility Quantitative Itemset Mining

The task of high utility itemset mining (HUIM) is useful but there is a major limitation, which is that the discovered high utility itemsets do not provide information about quantities. Thus, even though an itemset like {b,c,d} may be a high utility itemset, it does not indicate how many breads, how many cakes and how many dattes people like to buy together. But of course, buying 1 breads, 5 breads or 10 breads is not the same. Thus, it is important to have this information.

To address this limitation, the task of High Utility Quantitative Itemset Mining (HUQIM) was proposed. In this task, the discovered patterns provide information about quantities.

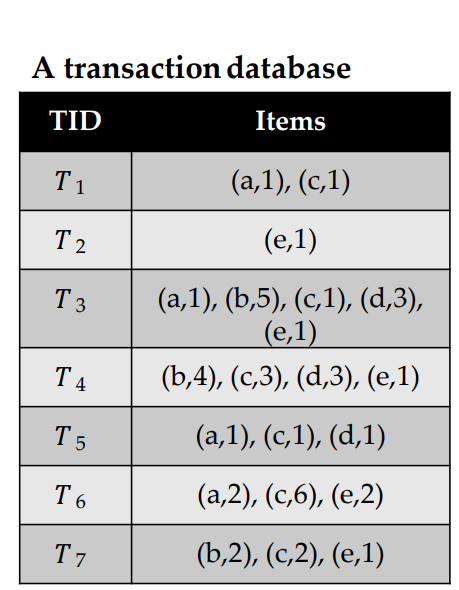
I will explain this with an example. Consider this database:

In HUQIM, we may find an itemset with quantities such as {(apple:2), (cake:2)} indicating that some people buy 2 apples with 2 cakes. But how to calculate the utility of this itemset? The utility is calculated as before but by only considering the transactions where a customer has bought 2 apples with 2cakes, that is T1 and T3:

The utility of {(apple:2), (cake:2)} in T1 is: (2 x 3) + (2 x 2), and the utility of that itemset in T3 is (2 x 3) + (2 x 2). Thus the utility of {(apple,2), (cake,2)} in the whole database is the sum of this: (2 x 3) + (2 x 2) + (2 x 3) + (2 x 2) = 20 $.

Such itemset where each item has an exact quantity is called an exact Q-itemset.

It is also possible to find another type of itemsets called the range Q-itemsets. Explained simply, a range Q-itemset is an itemset where quantities of items are expressed with some intervals. For example, the itemset {(bread,4,5),(cake,2,3)} means that some customer(s) buy 4 to 5 breads with 2 to 3 cakes. To compute the utility of this itemset is also simple. We first need to find all transactions where there are 4 to 5 breads with 2 to 3 cakes and calculate the utility (profit) and then do the sum. The two transactions meeting this criterion are T1 and T2:

Then, we multiply the quantity of bread and cake by their unit profits in these two transactions, which gives : (5 x 1) + (2 x 2) + (4 x 1) + (3 x 2) = 19 $

The problem of high utility quantitative itemset mining is interesting as it provides more information to the user than high utility itemset mining. However, the problem is also much more difficult because for each itemset like {b,c} multiple quantities may be assigned such as {(b,4),(c,3)}, {(b,5),(c,2)}, or even{(b,4,5),(c,3)}, etc. To avoid considering all possibilities, the algorithms for high utility quantitative itemset mining will use different combination methods to combine the quantities into ranges. There are a few combine methods like “combine_all”, “combine_min” and “Combine_max” that can be used. I will not explain them in this blog post to avoid going into too many details. Besides, there is also a parameter called “qrc” that is added to avoid making unecessary combinations.

In the end, the goal of high utility quantitative itemset is to find all the itemset with quantities that have a utility that is not less than the minutil threshold set by the user. I will just show a brief example of input and output:

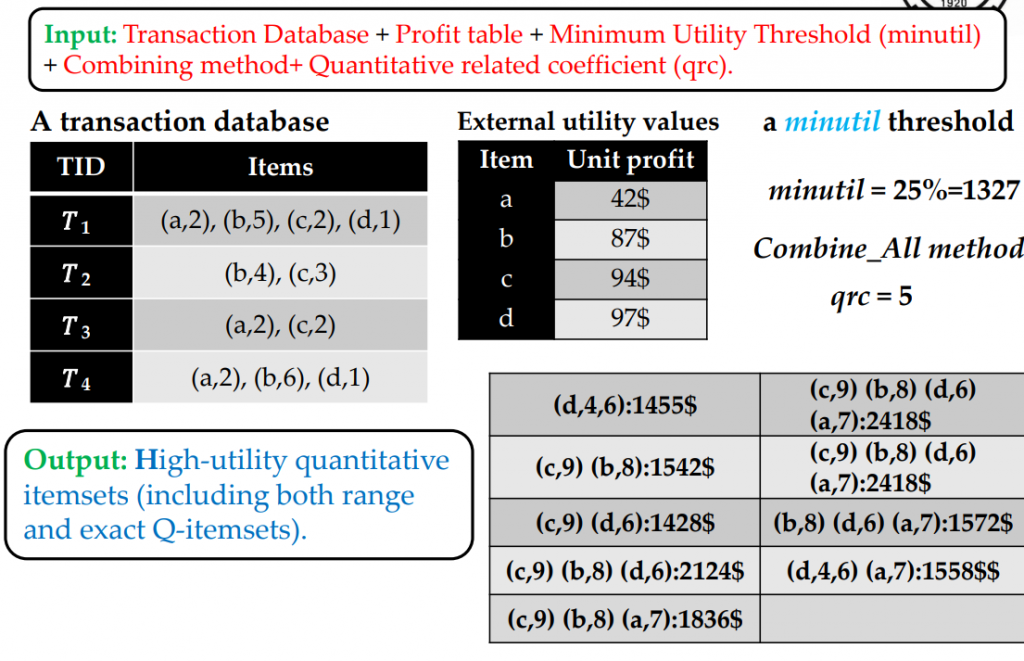
To find high utility quantitative itemsets, the main algorithms are:

• HUQA (2007), proposed in the paper “Mining high utility quantitative association rules”
• VHUQI (2014), presented in the paper “Vertical mining of high utility quantitative itemsets”.
• HUQI-Miner (2019), introduced in the paper “Efficient mining of high utility quantitative itemsets”
• FHUQI-MIner (2021): This is the most recent algorithm, which is the state-of-the-art. It was proposed in this paper: FHUQI-Miner: Fast High Utility Quantitative Itemset Mining. 

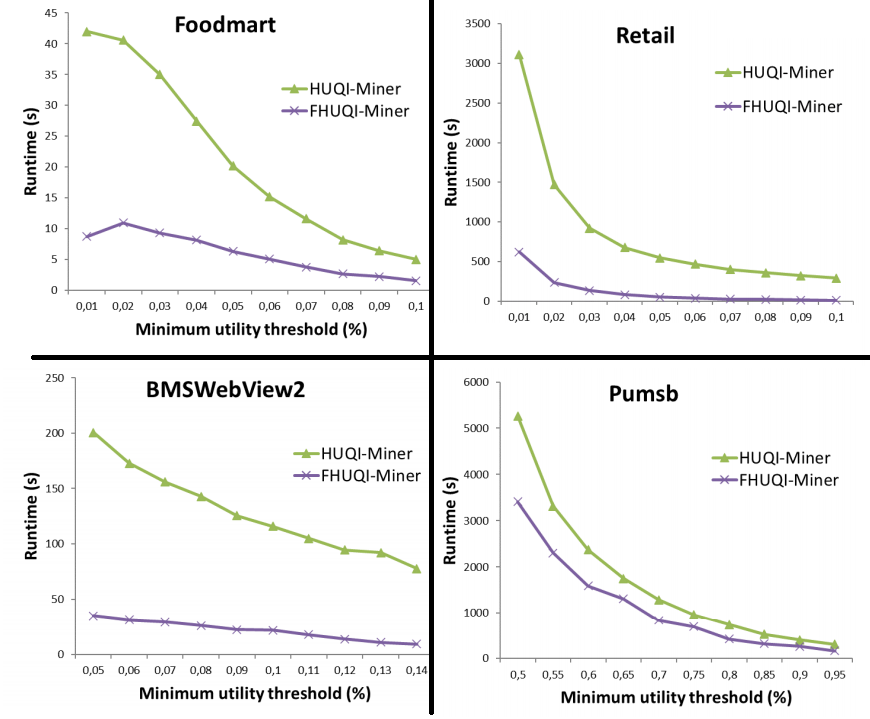
If you are new to this topic, reading the FHUQI-Miner paper is a good start as it is a journal paper that explains clearly all the important definitions with many examples. FHUQI-Miner was also shown to be much faster than the previous best algorithms in experiments, so it is good to start from this algorithm to develop extensions. Below is for example a performance comparison of FHUQI-Miner with the previous best algorithm called HUQI-Miner. It was found that FHUQI-Miner can be up to 20 times faster in some cases.

Also, you may find open-source implementations of several algorithms for HUQIM in the SPMF  open-source data mining software, with datasets.

It is also possible to study extensions of the problem of finding high utility quantitative itemsets. For example, here are two recent papers by my team where we extend FHUQI-Miner for variations of the problem:

• TKQ (2021) : Finding the top-k high utility quantitative itemsets : The idea is that rather than using the minutil parameter, the user can directly ask to find the k itemsets that yield the highest utility (e.g. the top 100 itemsets)
• CHUQI-Miner (2021): This is a recent algorithm to find correlated high utility quantitative itemsets. The motivation is that many itemsets may have a high utility but still be weakly correlated. By using the bond correlation measure, more meaningful itemsets may be found.

Conclusion

In this blog post, I introduced the problem of high utility quantitative itemset mining. Hope it has been interesting. The content of this blog post is based on the articles that I did with Dr. Mourad Nouioua, post-doc in my team, on FHUQI-Miner and his very detailled powerpoint presentation about this algorithm. If you have any comments, please leave it in the comment section below!

—
Philippe Fournier-Viger is a full professor working in China and founder of the SPMF open source data mining software.