Today, I will show how to draw the powerset of a set using Latex and TIKZ, to produce some nice figures that can be used in paper written using Latex. The code that is shown below is adapted from code from StackOverflow.
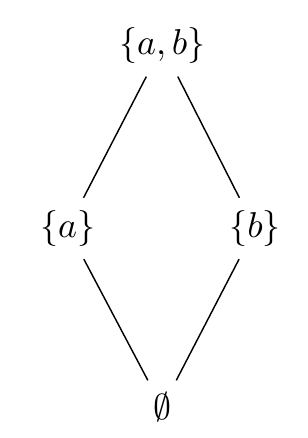
First, we will draw the powerset of the set {a,b} as a Hasse diagram:
\documentclass{article}
\usepackage{tikz-cd}
\begin{document}
\begin{tikzpicture}
\matrix (A) [matrix of nodes, row sep=1.2cm]
{
& $\{a,b\}$ \\
$\{a\}$ & & $\{b\}$\\
& $\emptyset$ \\
};
\draw (A-1-2)--(A-2-1);
\draw (A-1-2)--(A-2-3);
\draw (A-2-1)--(A-3-2);
\draw (A-2-3)--(A-3-2);
\end{tikzpicture}
\end{document}
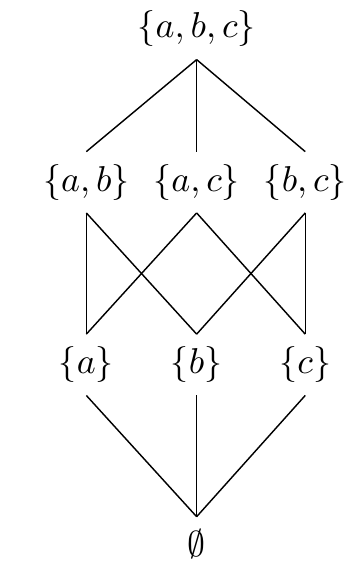
Then, I will show how to draw the powerset of the set {a,b,c}:
\documentclass{article}
\usepackage{tikz-cd}
\begin{document}
\begin{tikzpicture}
\matrix (A) [matrix of nodes, row sep=1.2cm]
{
$\{a,b\}$ & $\{a,c\}$ & $\{b,c\}$ \\
$\{a\}$ & $\{b\}$ & $\{c\}$ \\
& $\emptyset$ \\
};
\path (A-1-1)--(A-1-2) node[above=1.2cm] (link) {$\{a,b,c\}$};
\foreach \i in {1,...,3}
\draw (link.south) -- (A-1-\i.north);
\foreach \i/\j in {1/2, 3/2, 2/1, 1/1, 3/3, 2/3}
\draw (A-1-\i.south)--(A-2-\j.north);
\foreach \i/\j in {1/2, 2/2, 3/2}
\draw (A-2-\i.south)--(A-3-\j.north);
\end{tikzpicture}
\end{document}
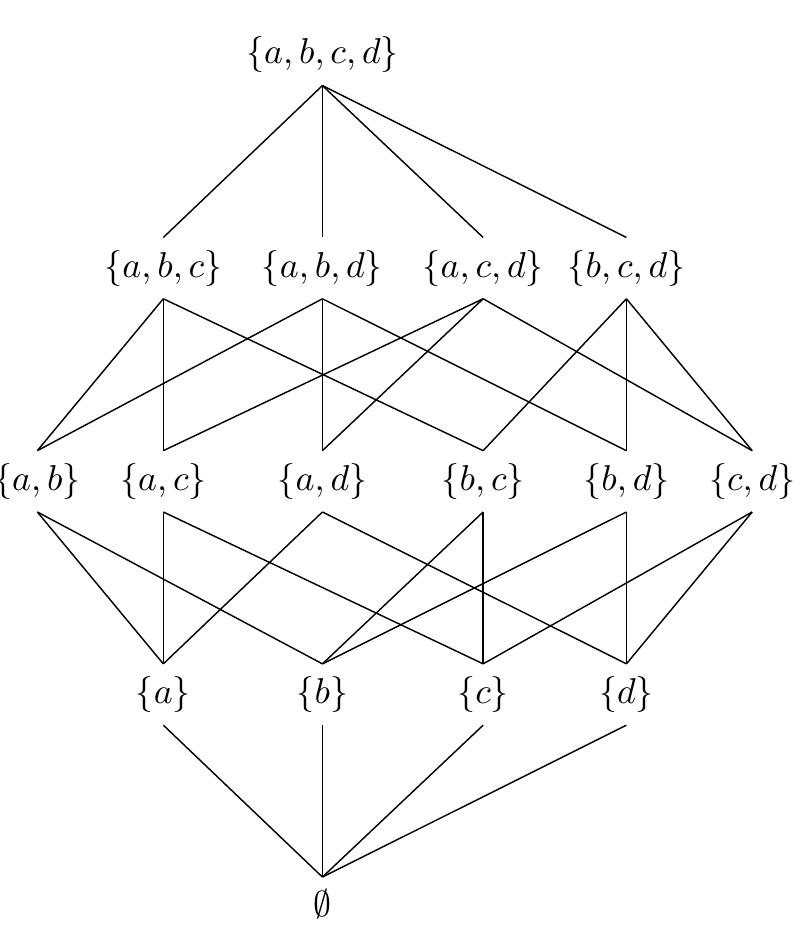
Then, I will show how to draw the powerset of the set {a,b,c,d}:
\begin{tikzpicture}
\matrix (A) [matrix of nodes, row sep=1.5cm]
{
~ & ~ & $\{a,b,c,d\}$ \\
~ & $\{a,b,c\}$ & $\{a,b,d\}$ & $\{a,c,d\}$ & $\{b,c,d\}$\\
$\{a,b\}$ & $\{a,c\}$ & $\{a,d\}$ & $\{b,c\}$ & $\{b,d\}$ & $\{c,d\}$\\
~ & $\{a\}$ & $\{b\}$ & $\{c\}$ & $\{d\}$\\
~ & ~ & $\emptyset$ \\
};
\draw (A-1-3.south)--(A-2-2.north);
\draw (A-1-3.south)--(A-2-3.north);
\draw (A-1-3.south)--(A-2-4.north);
\draw (A-1-3.south)--(A-2-5.north);
\draw (A-2-2.south)--(A-3-1.north);
\draw (A-2-2.south)--(A-3-2.north);
\draw (A-2-2.south)--(A-3-4.north);
\draw (A-2-3.south)--(A-3-1.north);
\draw (A-2-3.south)--(A-3-3.north);
\draw (A-2-3.south)--(A-3-5.north);
\draw (A-2-4.south)--(A-3-2.north);
\draw (A-2-4.south)--(A-3-3.north);
\draw (A-2-4.south)--(A-3-6.north);
\draw (A-2-5.south)--(A-3-4.north);
\draw (A-2-5.south)--(A-3-5.north);
\draw (A-2-5.south)--(A-3-6.north);
\draw (A-3-1.south)--(A-4-2.north);
\draw (A-3-1.south)--(A-4-3.north);
\draw (A-3-2.south)--(A-4-2.north);
\draw (A-3-2.south)--(A-4-4.north);
\draw (A-3-3.south)--(A-4-2.north);
\draw (A-3-3.south)--(A-4-5.north);
\draw (A-3-4.south)--(A-4-3.north);
\draw (A-3-4.south)--(A-4-4.north);
\draw (A-3-5.south)--(A-4-3.north);
\draw (A-3-5.south)--(A-4-5.north);
\draw (A-3-6.south)--(A-4-4.north);
\draw (A-3-6.south)--(A-4-5.north);
\draw (A-4-2.south)--(A-5-3.north);
\draw (A-4-3.south)--(A-5-3.north);
\draw (A-4-4.south)--(A-5-3.north);
\draw (A-4-5.south)--(A-5-3.north);
\end{tikzpicture}
Here is another diagram that I have done but this time using the TIKZ automata package instead:
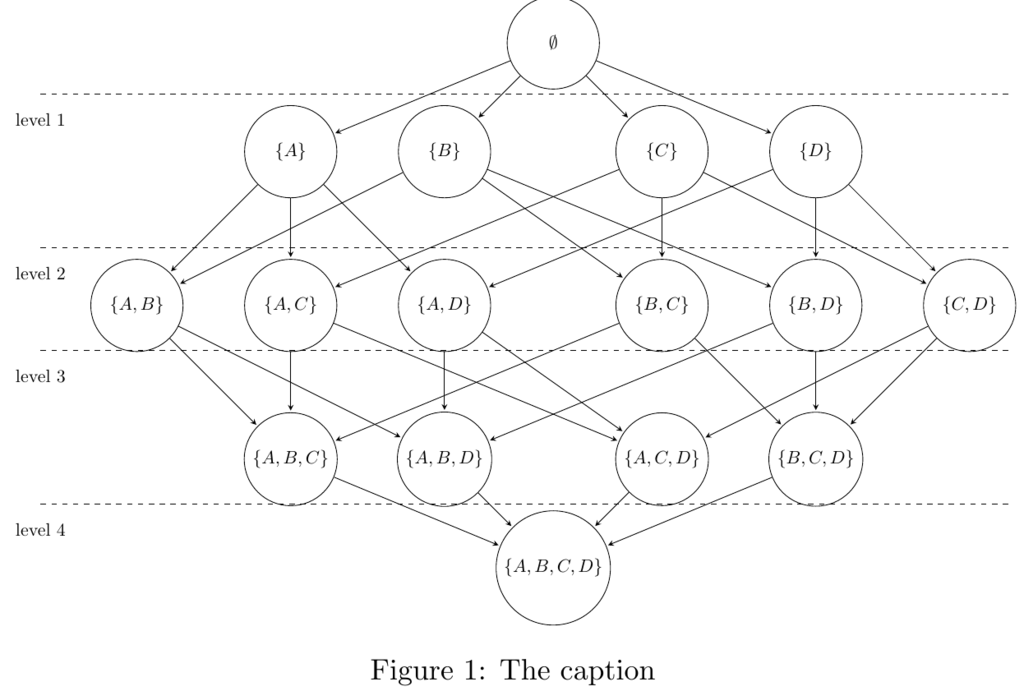
Here is the code:
\documentclass{article}
\usepackage{caption}
\usepackage{subcaption}
\usepackage{tikz}
\usetikzlibrary{automata,arrows,positioning,calc}
\begin{document}
\begin{figure}\centering
\resizebox{\columnwidth}{!}{
\begin{tikzpicture}[> = stealth, shorten > = 1pt, auto, node distance = 3cm,state/.style={circle, draw, minimum size=1.8cm}]
%%% LEVEL 1
\node[state] (x) {$\emptyset$};
%%% LEVEL 2
\node[state] [below left of=x] (B) {$\{ B \}$};
\node[state][below right of=x] (C) {$\{ C \}$};
\node[state] [left of=B] (A) {$\{ A \}$};
\node[state][right of=C] (D) {$\{ D \}$};
%%%% LEVEL 3
\node[state][below of=B] (AD) {$\{ A,D \}$};
\node[state][below of=C] (BC) {$\{ B,C \}$};
\node[state][below of=D] (BD) {$\{ B,D \}$};
\node[state][below of=A] (AC) {$\{ A,C \}$};
\node[state] [left of=AC] (AB){$\{ A,B \}$};
\node[state] [right of=BD] (CD){$\{ C,D \}$};
%% LEVEL 4
\node[state][below of=AD] (ABD) {$\{ A,B,D \}$};
\node[state][below of=BC] (ACD) {$\{ A,C,D \}$};
\node[state][left of=ABD] (ABC) {$\{ A,B,C \}$};
\node[state][right of=ACD] (BCD) {$\{ B,C,D \}$};
%%%% LEVEL 5
\node[state][below right of=ABD] (ABCD) {$\{ A,B,C,D \}$};
%% LEVEL 1 to LEVEL 2
\path[->] (x) edge node {} (A);
\path[->] (x) edge node {} (B);
\path[->] (x) edge node {} (C);
\path[->] (x) edge node {} (D);
%% LEVEL 2 to LEVEL 3
\path[->] (A) edge node {} (AB);
\path[->] (A) edge node {} (AC);
\path[->] (A) edge node {} (AD);
\path[->] (B) edge node {} (AB);
\path[->] (B) edge node {} (BC);
\path[->] (B) edge node {} (BD);
\path[->] (C) edge node {} (AC);%
\path[->] (C) edge node {} (BC);
\path[->] (C) edge node {} (CD);
\path[->] (D) edge node {} (AD);
\path[->] (D) edge node {} (BD);
\path[->] (D) edge node {} (CD);
%%% LEVEL 3 TO 4
\path[->] (AB) edge node {} (ABC);
\path[->] (AB) edge node {} (ABD);
\path[->] (AC) edge node {} (ABC);
\path[->] (AC) edge node {} (ACD);
\path[->] (AD) edge node {} (ABD);
\path[->] (AD) edge node {} (ACD);
\path[->] (BC) edge node {} (ABC);
\path[->] (BC) edge node {} (BCD);
\path[->] (BD) edge node {} (ABD);
\path[->] (BD) edge node {} (BCD);
\path[->] (CD) edge node {} (ACD);
\path[->] (CD) edge node {} (BCD);
%%%% LEVEL 4 to 5
\path[->] (ABC) edge node {} (ABCD);
\path[->] (ABD) edge node {} (ABCD);
\path[->] (ACD) edge node {} (ABCD);
\path[->] (BCD) edge node {} (ABCD);
%%%% Dashed lines
\draw[dashed] (-10,-1) -- (9,-1);
\draw[dashed] (-10,-4) -- (9,-4);
\draw[dashed] (-10,-6) -- (9,-6);
\draw[dashed] (-10,-9) -- (9,-9);
\node[] at (-10,-1.5) {level 1};
\node[] at (-10,-4.5) {level 2};
\node[] at (-10,-6.5) {level 3};
\node[] at (-10,-9.5) {level 4};
\end{tikzpicture}
}
\caption{The caption}
\end{figure}
\end{document}
That is all for today. Hope this will be useful.
Note that I had also written a blog post about how to draw the powerset of a set using Java and GraphViz instead of using Latex.