In this blog post, I will explain and provide source code to automatically draw the powerset of a set using Java and GraphViz. Drawing a powerset is useful in mathematics and also in computer science, for example in frequent itemset mining, it can be used to visualize relationships between itemsets.
What is the powerset of a set?
It can be simply defined as a set and all its subsets.
For example, the powerset of the set {1,2,3} is the set { {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3} {1,2,3}}. It can be easily demonstrated that the size of a powerset of a set containing n items is 2^n.
How can we draw a powerset?
A powerset is often represented as a Hasse Diagram. For the purpose of drawing powersets, a Hasse Diagram can be defined as a diagram where:
- each vertex is a set from the powerset
- there is an edge from a set X to a set Y iff X ⊂ Y and there does not exist a set Z such that X ⊂ Z ⊂ Y
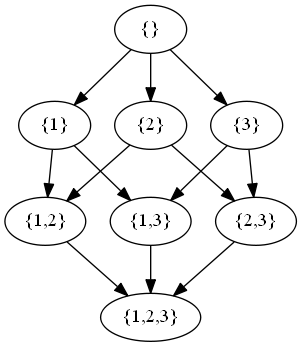
For example, the Hasse diagram of the powerset of {1,2,3} is:
Now, I will show how to draw a nice diagram automatically such as the one above.
Step 1. Generate a GraphViz input file
The first step is to have Java installed on your computer and use the following Java program to generate a GraphViz input file named “input.dot” for the powerset of {a,b,c,d,e}. Note that you can edit the line String[] set = new String[] { “a”, “b”, “c”, “d”, “e” } to draw the powerset of another set. Note also that the Java code below is not fully optimized. But for the purpose of drawing powersets, it is ok.
import java.io.BufferedWriter;
import java.io.FileWriter;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
/**
* @author Philippe Fournier-Viger, 2014
*/
public class DrawPowerSet {
public static void main(String[] arg) throws IOException,
InterruptedException {
// This is the set of integers that we want to draw the powerset of
String[] set = new String[] { "a", "b", "c", "d", "e" };
// output file
String output = "input.dot";
// create the file
BufferedWriter writer = new BufferedWriter(new FileWriter(output));
writer.write("digraph mygraph{");
// We will enumerate all the subset
for (long i = 0, max = 1 << set.length; i < max; i++) {
// we create a new subset
List newSet = new ArrayList();
for (int j = 0; j < set.length; j++) {
// check if the j bit is set to 1
int isSet = (int) i & (1 << j); if (isSet > 0) {
// if yes, add it to the set
newSet.add(set[j]);
}
}
// For the new subset, print links to all supersets
if (newSet.size() != set.length) {
printLinksToImmediateSupersets(newSet, set, writer);
}
}
// write end of file
writer.write("}");
writer.close();
}
/**
* This method print links from a subset to all its immediate supersets (not
* optimized).
*
* @param subset
* the subset
* @param set
* the set of all integers
* @param writer
* object to write to the output file
* @throws IOException
*/
private static void printLinksToImmediateSupersets(List subset,
String[] set, BufferedWriter writer) throws IOException {
// For each integer in the set of all integers
for (int i = 0; i < set.length; i++) {
String value = set[i];
// if it is not contained in the subset
if (subset.contains(value) == false) {
// we add it to the set to make an immediate superset
// and write the link
List newSet = new ArrayList();
newSet.addAll(subset);
newSet.add(value);
writer.write(asString(subset) + " -> " + asString(newSet)
+ " \n");
}
}
}
/**
* Convert a set to a string representation
*
* @param set
* the set as a list of integers
* @return a string
*/
private static String asString(List set) {
Collections.sort(set);
// if the empty set, we will write "{}"
if (set.size() == 0) {
return "\"{}\"";
}
// otherwise we will write the set of integers
StringBuffer buffer = new StringBuffer();
buffer.append("\"{");
// for each integer
for (int i = 0; i < set.size(); i++) {
String value = set.get(i);
buffer.append(value);
if (i != set.size() - 1) {
buffer.append(",");
}
}
buffer.append("}\"");
return buffer.toString();
}
}
By running the above program, it will create a file called input.dot containing a content similar to this, which represents the nodes of the graph that will be drawn and the links between nodes.
digraph mygraph{"{}" -> "{a}"
"{}" -> "{b}"
"{}" -> "{c}"
"{}" -> "{d}"
"{}" -> "{e}"
"{a}" -> "{a,b}"
"{a}" -> "{a,c}"
....
"{c,d,e}" -> "{a,c,d,e}"
"{c,d,e}" -> "{b,c,d,e}"
"{a,c,d,e}" -> "{a,b,c,d,e}"
"{b,c,d,e}" -> "{a,b,c,d,e}"
}
Step 2. Generating a PNG file of the graph using GraphViz
Then, we can run GraphViz from the command line to generate the graph as a PNG file:
dot -Tpng input.dot > output.png"
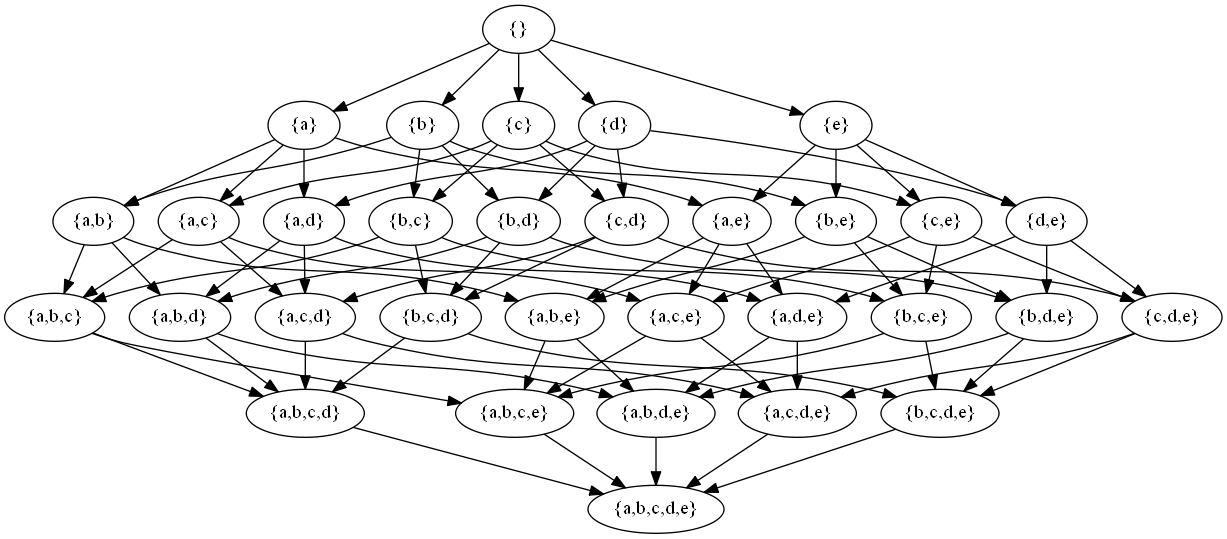
This will generate a nice Hasse Diagram:
—
Hope that you have enjoyed this post. If you like this blog, you can tweet about it and/or subscribe to my twitter account @philfv to get notified about new posts.
Philippe Fournier-Viger is an assistant professor in Computer Science and also the founder of the open-source data mining software SPMF, offering more than 52 data mining algorithms.





Hello and thanks for making spmf. I’m starting to use it in my research as I can see several applications of pattern mining being useful for it.
What I’m looking to do now is create Hasse Diagrams of the frequent closed itemsets that can be mined using spmf. Since my ground sets are quite large and the itemset structure is quite complex, I need a smart algorithm to do so.
Is there any implementantion out there you can point me to ? Or do I have to write my own ? If so, how do the support of the itemset and its “size” (cardinality) come into play in making a good algorithm to create this graph.
Thanks!
Hello, You are welcome. I am glad that SPMF is useful.
For drawing the Hasse diagram of closed itemsets, I don’t know any code that do that. But you could probably easily write some code and use for example GraphViz to draw the diagram. Graphviz is not too difficult to use. I am not sure thought if it would work well if you have too many itemsets. But you can try.
To write your own, you could:
– use a closed itemset mining algorithm to first extract the closed itemset (you can use SPMF for that).
– then, to draw the graph, you should draw a line from an itemset X to an Y if and only if X is a subset of Y and there exists no itemset Z such that X is a subset of Z and Z is a subset of Y. How to draw these lines could be a little bit tricky. But in my opinion, performance should not be too much of an issue, unless you are drawing thousands of itemsets. So maybe you could just use a brute force algorithm where you compare each itemset X1 with all its supersets and then draw the lines. Then you could consider a second itemset X2, and find all its supersets and draw the lines, Then you could consider a third itemset X3 and find all its supersets and draw the lines… etc. That would be a simple approach. If you think more about this problem, maybe that you could find other optimizations if speed is an issue.
Then you could generate the graphviz file
– Then you could draw the graph using graphviz.
Besides Graphviz, there exists some libraries for drawing different kinds of graph with Java, if you want to do some more programming.
This is my advices. Personally, I would probably just use Graphviz.
Best regards
Pingback: Drawing the Powerset of a Set using Latex and TIKZ (Hasse Diagram) | The Data Mining Blog