This is a very short blog post about the calculation of the number of possible association rules in a dataset. I will assume that you know already what is association rule mining.
Let’s say that you have a dataset that contains r distinct items. With these items, it is possible to make many rules. Since the left side and right side of a rule cannot be empty, then the left side of a rule can contain between 1 to r-1 items (since the right side of a rule cannot be empty). Lets say that the number of items on the left size of a rule is called k and that the number of items on the right size is called j.
Then, the total number of association rules that can be made from these r items is:
For example, lets say that we have r = 6 distinct items. Then, the number of possible association rules is 602.
This may seems a quite complex expression but it is correct. I have first seen it in the book “Introduction to Data Mining” of Tan & Kumar. If you want to type this expression in Latex, here is the code:
\sum_{k=1}^{r-1}\left[\binom{r}{k} \times \sum_{j=1}^{r-k}\binom{r-k}{j}\right] = 3^r - 2^{r+1}+1
By the way, this expression is also correct for counting the number of possible partially-ordered sequential rules or partially-ordered episode rules.
Related to this, the number of itemsets that can be made from a transaction dataset having r distinct items is:
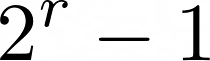
In that expression, the -1 is because we exclude the empty set. Here is the Latex code for that expression:
2^{r}-1
Conclusion
This was just a short blog post about pattern mining to discuss the size of the search space in association rule mining. Hope you have enjoyed it.
—
Philippe Fournier-Viger is a full professor working in China and founder of the SPMF open source data mining software.
