Today, I will talk about pattern mining. I will explain a topic that is in my opinion very important but has been largely overlooked by the research community working on high utility itemset mining. It is to integrate length constraints in high utility itemset mining. The goal is to find patterns that have a maximum size, defined by the user (e.g. no more than two items).
Why do this? There are two very important reasons.
First, from a practical perspective, it is often unnecessary to find the very long patterns. For example, let’s say that we analyze shopping data and find that a high utility pattern is that people buy {mapleSyrup, pancake, orange, cheese, cereal} together and that this yield a high profit. This may sound like an interesting discovery, but from a business perspective, it is not useful as this pattern contain too many items. For example, it would not be easy for a business to do marketing to promote buying 5 items together. This has been confirmed in my discussion with a business in real-life. I was told by someone working for a company that they are not interested in patterns with more than 2 or 3 items.
Second, finding the very long patterns is inefficient due to the very large search space. They are generally too many possible combinations of items. If we add a constraint on the length of patterns to be found, then we could save a huge amount of time to focus on the small patterns that are often more interesting for the user.
Based on these motivations, some algorithms like FHM+ and MinFHM have focused on finding the small patterns that have a high utility using two different approaches. In this blog post, I will give a brief introduction to the ideas from those algorithms, which could be integrated in other pattern mining problems.
First, I will give a brief introduction about high utility itemset mining for those who are not so familiar with this topic and then I will explain the solutions to find short patterns that are proposed in those algorithms.
High utility itemset mining
High utility itemset mining is a data mining task that aim at finding patterns in a database that have a high importance. The importance of a pattern is measured using a utility function. There can be many applications of high utility itemset mining, but the classical example is to find the sets of products purchased together by customers in a store that yield a high profit (utility). In that setting, the input is a transaction database, that is a set of records (transactions) indicating the items that some customers have bought at different times. For example, consider the following transaction database, which contains seven transactions called T1, T2, T3… T5:
The second transaction T2 indicates that a customer has bought 4 units of an item “b” which stands for Bread and 3 units of an item “c”, which stands for Cake, 3 units of an item “d” which stands for Dates, and 1 unit of an item “e”, which stands for “Egg”. The second transaction contains 1 unit of an item “a”, denoting “Apple”, 1 cake and 1 unit of Dates. Besides, that table, another table is provided indicating the relative importance of each item. In this example, that table indicate the unit profit of each item (how much money is earned by the sale of 1 unit):
This table for example indicates that the sale of 1 Apple yields a 5$ profit, the sale of 1 bread yields 2$ profit, and so on.
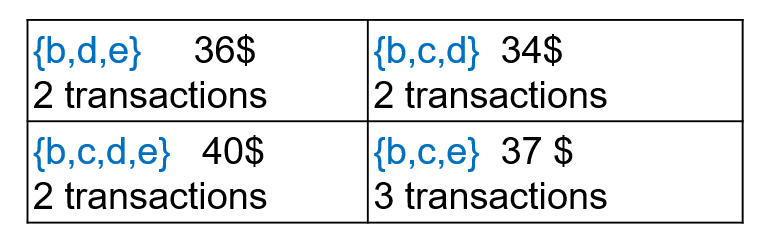
To do the task of high utility itemset mining, the user must set a threshold called the minimum utility threshold (minutil). The goal is to find all the itemsets (sets of items) that have a utility (profit) that is no less than that threshold. For example, if the user set the threshold as minutil = 33$, there are four high utility itemsets:
The first itemset {b,d,e} means that customers buying Bread, Dates and Eggs together yield a total utility (profit) of 36$ in this database. It is a high utility itemset because 36$ is no less than minutil = 33$. But how do we calculate the utility of an itemset in a database? It is not very complicated. Let me show you. Let’s say that we take the itemset {b,d,e} as example. These items are purchased together in the transactions T1 and T2 of the database, which are highlighted below:
To calculate the utility of {b,d,e}, we need to multiply the quantities associated with b,d,e in T1 and T2 by their unit profit. This is done as follow:
In T1, we have: (5 x 2) + (3 x 2) + (1 x 3) = 19 $ because the customer bought 5 breads for 2$ each, 3 dates for 2 $ each and 1 egg for 1 $.
In T2, we have (4 x 2) + (3 x 2) + (1 x 3) = 17 $ because the customer bought 5 breads for 2$ each, 3 dates for 2 $ each and 1 egg for 1 $.
Thus, the total profit of {b,d,e} for T1 and T2 is 19$ + 17 $ = 36 $.
The problem of high utility itemset mining has been widely studied in the last two decades. Besides the example of shopping above, it can be applied to many other problems as the letters like a,b,c,d,e could represent for example webpages or words in a text. There has been many efficient algorithms that have been designed for high utility itemset mining such as IHUP, UP-Growth, HUI-Miner*, FHM, EFIM, ULB-Miner and REX to name a few. If you are interested by this topic, I wrote a good survey that introduce the problem in more details and it is easy to understand for beginners in this field.
Finding the Minimal High Utility Itemsets with MinFHM
As I said in the introduction, a problem with high utility itemset mining is that many high utility itemsets are very long and thus not useful in practice. This leads to finding too many patterns and to very long runtimes.
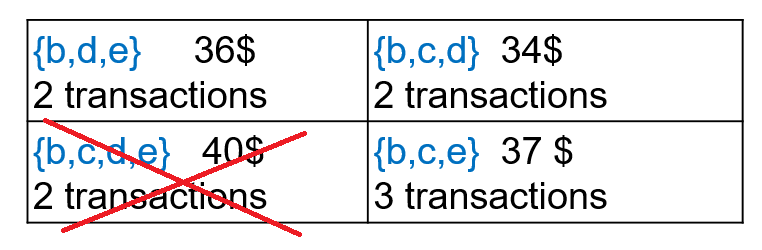
The first solution to this problem was proposed in the MinFHM algorithm. It is to find the minimal high utility itemsets. A minimal high utility itemset is simply a high utility itemset that is not a subset of a larger high utility itemset. This definition allows to focus on the smallest sets of items that yield a high utility (e.g. profit in this example). For example, if we take the same database and minutil = 33$, there are only threeminimal high utility itemsets:
The itemset {b,c,d,e} is not a minimal high utility itemsets because it has subsets such as {b,d,e} that are high utility itemsets.
To find the minimal high utility itemsets, MinFHM is a modified version of the FHM algorithm. It relies on search space reduction techniques that are specially designed to find the minimal high utility itemsets. This led to not only finding less patterns than FHM but also on having much faster runtimes. On some benchmark datasets, MinFHM was for example up to 800 times faster than FHM and could find up to 900,000 times less patterns.
For researchers, something interesting about the problem of minimal high utility itemsets is the following two properties, which are somewhat special for this problem:
I will not talk too much about the details of this as my goal is just to give some introduction. For more details about MinFHM, you can see the paper, powerpoint, video presentation and source code, below:
Fournier-Viger, P., Lin, C.W., Wu, C.-W., Tseng, V. S., Faghihi, U. (2016). Mining Minimal High-Utility Itemsets. Proc. 27th International Conference on Database and Expert Systems Applications (DEXA 2016). Springer, LNCS, pp. 88-101. [ppt] [source code]
DOI: 10.1007/978-3-319-44403-1_6
Finding the High Utility Itemsets with a length constraint with FHM+
Now, let me talk about another solution to find the short high utility itemsets. This solution consists of simply adding a new parameter that sets a maximum length on the patterns to be found. For example, if take the same example and say that minutil = 33$ and the maximum length is 3, then the following three high utility itemsets are found:
In this example, the results is the same as the minimal high utility itemsets but it is not always the case.
To find the high utility itemsets with a length constraint, a naïve solution is to filter out the high utility itemsets that are too long as a post-processing step after applying a traditional high utility itemset mining algorithm such as FHM. However, that would not be efficient. For this reason, I have proposed the FHM+ algorithm in previous work. It is a modified version of FHM. The key idea is as follows. The FHM algorithm just like other high utility itemset mining algorithms uses upper bounds on the utility to reduce the search space such as the TWU and remaining utility (which I will not explain here). These upper bounds are defined by assuming that all items of a transaction could be used to create high utility itemsets. But if we have a length constraints and know that lets say we don’t want to find patterns with more than 3 items, then we can greatly reduce these upper bounds. This allows to reduce a much larger part of the search space and thus to have a much faster algorithm!
In the FHM+ paper, I have shown that using these ideas, the memory usage can be reduced by up to 50%, the speed can be increased by up to 4 times and up to 2700 times less patterns can be discovered, on benchmark datasets!
This is just a brief introduction, and these ideas could be used in other pattern mining problems. For more details, you may see the paper, powerpoint presentation and code below:
Fournier-Viger, P., Lin, C.W., Duong, Q.-H., Dam, T.-L. (2016). FHM+: Faster High-Utility Itemset Mining using Length Upper-Bound Reduction. Proc. 29th Intern. Conf. on Industrial, Engineering and Other Applications of Applied Intelligent Systems (IEA AIE 2016), Springer LNAI, pp. 115-127. [ppt] [source code]
Conclusion
In this blog post, I have explained why it is unnecessary to find the very long patterns in high utility itemset mining for some applications such as analyzing customer behavior. I have also shown that if we focus on short patterns, we can greatly improve the runtimes and also reduce the number of patterns shown to the user. This can bring the algorithms for high utility itemset mining closer to what users really need in real-life. I have discussed two solutions to find short patterns, which are to find minimal high utility itemsets and using a length constraint.
That is all for today!
—
Philippe Fournier-Viger is a distinguished professor of computer science and founder of the SPMF open-source data mining library, which offers over 200 algorithms for pattern mining.