On this blog, I have previously given an introduction to a popular data mining task called high utility itemset mining. Put simply, this task aims at finding all the sets of values (items) that have a high importance in a database, where the importance is evaluated using a numeric function. That sounds complicated? But it is not. A simple application is for example to analyze a database of customer transaction to find the sets of products that people buy together and yield a lot of money (values = purchased products, utility = profit). Finding such high utility patterns can then be used to understand the customer behavior and take business decisions. There are also many other applications.
High utility itemset mining is an interesting problem for computer science researchers because it is hard. There are often millions of ways of combining values (items) together in a database. Thus, an efficient algorithm for high utility itemset mining must search to find the solution (the set of high utility itemsets) while ideally avoid exploring all the possibilities.
To efficiently find a solution to a high utility itemset mining problem (task), several efficient algorithms have been designed such as UP-Growth, FHM, HUI-Miner, EFIM, and ULB-Miner. These algorithms are complete algorithms because they guarantee finding the solution (all high utility itemsets) However, these algorithms can still have very long execution times on some databases depending on the size of the data, the algorithm’s parameters, and the characteristics of the data.
For this reason, a research direction in recent years has been to also design some approximate algorithms for high utility itemset mining. These algorithms do not guarantee to find the complete solution but try to be faster. Thus, there is a trade-off between speed and completness of the results. Most approximate algorithms for high utility itemset mining are based on optimization algorithms such as those for particle-swarm optimization, genetic algorithms, the bat algorithm, and bee swarm optimization.
Recently, my team proposed a new paper in that direction to appear in 2021, where we designed two new approximate algorithms, named HUIM-HC and HUIM-SA, respectively based on Hill Climbing and Simulated Annealing. The PDF of the paper is below:
Nawaz, M.S., Fournier-Viger, P., Yun, U., Wu, Y., Song, W. (2021). Mining High Utility Itemsets with Hill Climbing and Simulated Annealing. ACM Transactions on Management Information Systems (to appear)
In that paper, we compare with many state-of-the art approximate algorithms for this problem (HUIF-GA, HUIM-BPSO, HUIM-BA, HUIF-PSO- HUIM-BPSOS and HUIM-GA) and observed that HUIM-HC all algorithms on the tested datasets. For example, see some pictures from some runtime experiments below on 6 datasets:
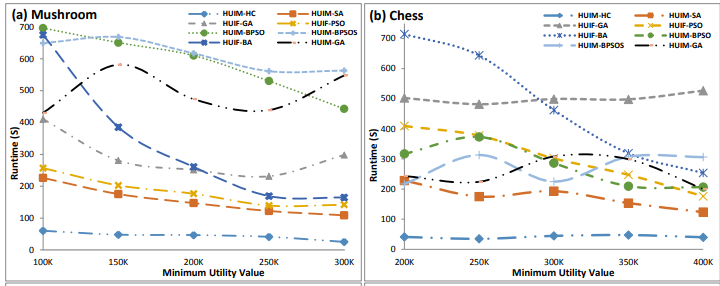
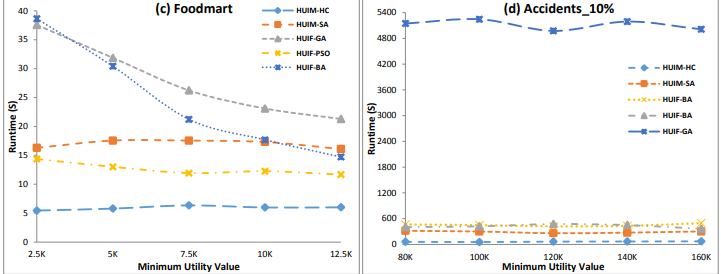
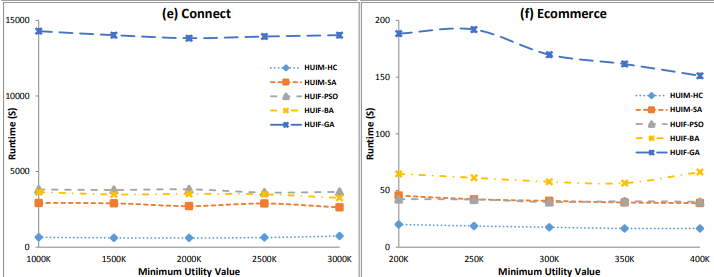
In this picture, it can be observed that HUIM-SA and HUIM-HC have excellent performance. In a) b) c) d), e), f) HUIM-HC is the fastest, while HUIM-SA is second best on most datasets (except Foodmart).
In another experiment in the paper it is shown that although HUIM-SA is usually much faster than previous algorithms, it can find about the same number of high utility itemsets, while HUIM-HC usually find a bit less.
If you are interested by this research area, there are several possibilities for that. A good starting point to save time is to read the above paper and also you can find the source code of all the above algorithms and datasets in the SPMF data mining library. By using that source code, you do not need to implement these algorithms again and can compare with them. By the way, the source code of HUIM-HC and HUIM-SA will be included in SPMF next week (as I still need to finish the integration).
Hope that this blog post has been interesting! I did not write so much on the blog recently because I have been very busy and some unexpected events occurred. But now I have more free time and I will start again to write more on the blog. If you have any comments or questions, please write a comment below.
—
Philippe Fournier-Viger is a professor of Computer Science and also the founder of the open-source data mining software SPMF, offering more than 120 data mining algorithms.





Pingback: The SPMF data mining library v.2.40 is released! | The Data Mining Blog