Rankings are made in many fields, as we naturally tend to rank objects, persons or things, in different contexts. For example, in a singing or a sport competition, some judges will rank participants from worst to best and give prizes to the best participants. Another example is persons that rank movies or songs according to their tastes on a website by giving them scores.
If one has ranking data from several persons, it is possible that the rankings appear quite different. However, using appropriate techniques, it is possible to extract information that is common to several ranking that can help to understand the rankings. For example, although a group of people may disagree on how they rank movies, many people may agree that Jurassic Park 1 was much better than Jurassic Park 2. The task of finding subrankings common to several rankings is a problem called frequent subranking mining. In this blog post, I will give an introduction to this problem. I will first describe the problem and some techniques that can be used to mine frequent subrankings.
The problem of subranking mining
The input of the frequent subranking mining problem is a set of rankings. For example, consider the following database containing four rankings named r1, r2, r3and r4 where some food items are ranked by four persons.
| Ranking ID | Ranking |
| r1 | Milk < Kiwi < Bread < Juice |
| r2 | Kiwi < Milk < Juice < Bread |
| r3 | Milk < Bread < Kiwi < Juice |
| r4 | Kiwi < Bread < Juice < Milk |
The first ranking r1 indicates that the first person prefers juice to bread, prefers bread to kiwi, and prefers kiwi to milk. The other lines follow the same format.
To discover frequent subrankings, the user must specify a value for a parameter called the minimum support (minsup). Then, the output is the set of all frequent subrankings, that is all subrankings that appear in at least minsup rankings of the input database. Let me explain this with an example. Consider the ranking database of the above table and that minsup = 3. Then, the subranking Juice < Milk is said to be a frequent subranking because it appears at least 3 times in the database. In fact, it appears exactly three times as shown below:
| Ranking ID | Ranking |
| r1 | Milk < Kiwi < Bread < Juice |
| r2 | Kiwi < Milk < Juice < Bread |
| r3 | Milk < Bread < Kiwi < Juice |
| r4 | Kiwi < Bread < Juice < Milk |
The number of occurrence of a subranking is called its support (or occurrence frequency). Thus the support of he subranking Milk < Juice is 3. Another example is the subranking Kiwi < Bread < Juice which has a support of 2, since it appears in two rankings of the input database:
| Ranking ID | Ranking |
| r1 | Milk < Kiwi < Bread < Juice |
| r2 | Kiwi < Milk < Juice < Bread |
| r3 | Milk < Bread < Kiwi < Juice |
| r4 | Kiwi < Bread < Juice < Milk |
Because he support of Kiwi < Bread < Juice is less than the minimum support threshold, it is NOT a frequent subranking.
To give a full example, if we set minsup = 3, the full set of frequent subrankings is:
Milk < Bread support : 3
Milk < Juice support : 3
Kiwi < Bread support : 3
Kiwi < Juice support : 4
Bread < Juice support : 3
In this example, all frequent subrankings contains only two items. But if we set minsup = 2, we can find some subranking containing more than two items such as Kiwi < Bread < Juice, which has a support of 2.
This is the basic idea about the problem of frequent subranking mining, which was proposed in this paper:
Henzgen, S., & Hüllermeier, E. (2014). Mining Rank Data. International Conference on Discovery Science.
Note that in the paper, it is also proposed to then use the frequent subrankings to generate association rules.
How to discover the frequent subrankings?
In the paper by Henzgen & Hüllermeier, they proposed an Apriori algorithm to mine frequent subrankings. However, it can be simply observed that the problem of subrank mining can already be solved using the existing sequential pattern mining algorithms such as GSP (1996), PrefixSpan (2001), CM-SPADE (2014), and CM-SPAM (2014). This was explained in an extended version of the “Mining rank data” paper published on Arxiv (2018) and other algorithms specially designed for subranking mining were proposed.
Thus, one can simply apply sequential pattern mining algorithms to solve the problem. I will show how to use the SPMF software for this purpose. First, we need to encode the ranking database as a sequence database. I have thus created a text file called kiwi.txt as follows:
@CONVERTED_FROM_TEXT
@ITEM=1=milk
@ITEM=2=kiwi
@ITEM=3=bread
@ITEM=4=juice
1 -1 2 -1 3 -1 4 -1 -2
2 -1 1 -1 4 -1 3 -1 -2
1 -1 3 -1 2 -1 4 -1 -2
2 -1 3 -1 4 -1 1 -1 -2
In that format, each line is a ranking. The value -1 is a separator and -2 indicates the end of a ranking. Then, if we apply the CM-SPAM implementation of SPMF with minsup = 3, we obtain the following result:
milk -1 #SUP: 4
kiwi -1 #SUP: 4
bread -1 #SUP: 4
juice -1 #SUP: 4
milk -1 bread -1 #SUP: 3
milk -1 juice -1 #SUP: 3
kiwi -1 bread -1 #SUP: 3
kiwi -1 juice -1 #SUP: 4
bread -1 juice -1 #SUP: 3
which is what we expected, except that CM-SPAM also outputs single items (the first four lines above). If we dont want to see the single items, we can apply CM-SPAM with the constraint that we need at least 2 items, then we get the exact result of all frequent subrankings:
milk -1 bread -1 #SUP: 3
milk -1 juice -1 #SUP: 3
kiwi -1 bread -1 #SUP: 3
kiwi -1 juice -1 #SUP: 4
bread -1 juice -1 #SUP: 3
We can also apply other constraints on subrankings such as a maximum number of items using CM-SPAM. If you want to try it, you can download SPMF, and follows the instructions on the download page to install it. Then, you can create the kiwi.txt file, and run CM-SPAM as follows:
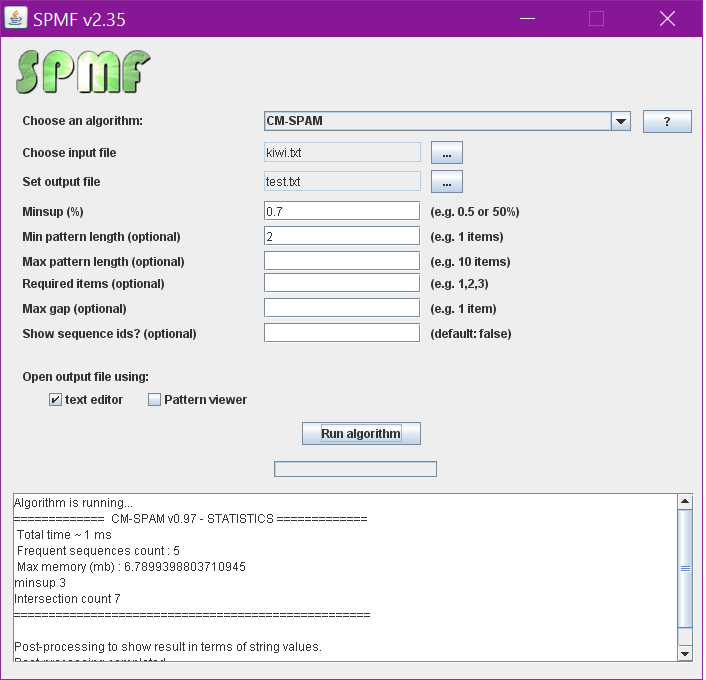
You will notice that in the above window, the minsup parameter is set to 0.7 instead of 3. The reason is that in the SPMF implementation, the minimum support is expressed as a percentage of the number of ranking (sequences) in the database. Thus, if we have 4 rankings, we multiply by 0.7, and we also obtain that minsup is equal to 3 rankings (a subranking will be considered as frequent if it appears in at least 3 rankings of the database).
What is also interesting, is that we can apply other sequential pattern mining algorithms of SPMF to find different types of subrankings: VMSP to find the maximal frequent subrankings, CM-CLASP to find the closed subrankings, or even VGEN to find the generator subrankings. We could also apply sequential rule mining algorithms such as RuleGrowth and CMRules to find rules between subrankings.
Conclusion
In this blog post, I discussed the basic problem of mining subrankings from rank data and that it is a special case of sequential pattern mining.
—
Philippe Fournier-Viger is a full professor working in China and founder of the SPMF open source data mining software.




