Introduction to Rare Itemset Mining

In the last decades, many data mining algorithms were developed to find interesting patterns in data (pattern mining). In particular, a lot of studies have been done about discovering frequent patterns (patterns that appear frequently) in a data. A classic example of this type of problem is frequent itemset mining, which aims at finding sets of values that frequently appear together in a database. This data mining task has many applications. For instance, it can be used to find all the itemsets (sets of products) that customers buy frequently in a database of customer transactions.Though discovering frequent patterns in data has many applications, there is an underlying assumption that patterns that frequently appear in data are important. But in real-life that is not always the case. For example, by analyzing data from a store, we may find that people very frequently buy bread and milk together but this pattern may not be interesting because it is very common, and thus it is not surprising at all that customers buy these products together.

Thus, in some cases, it is interesting to search for patterns in data that are rare. Finding rare patterns has thus drawn the interest of many researchers. It has for example applications such as to study rare diseases, rare occurrences of network failures, and suspicious behavior.In this blog post, I will thus talk about the problem of finding patterns in data that are infrequent (rare), which is known as the problem of rare itemset mining.

Some important definitions

To explain what is rare itemset mining, let me first introduce some definitions. To make it easy to understand, I will explain using the example of analyzing shopping data. But rare itemset mining is not limited to this application. Let take for example the table below, which shows a database of customer transactions made in a store by different customers:

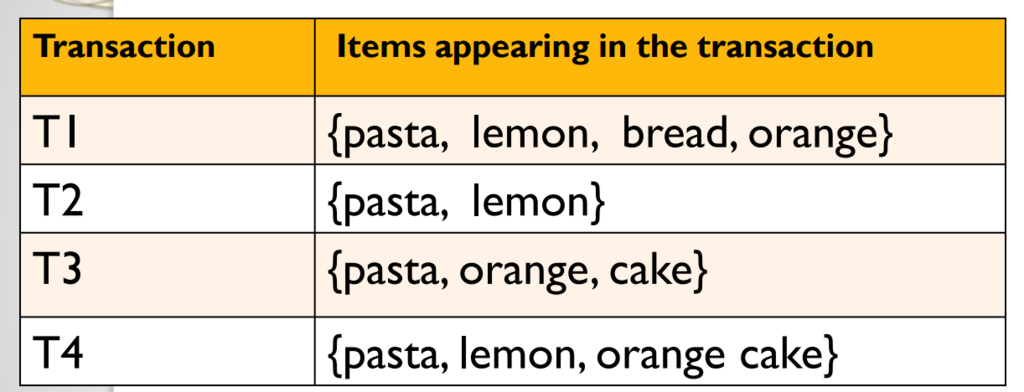
This database contains four transactions called T1, T2, T3 and T4, corresponding to four customers. The first transaction (T1) indicates that a customer has bought pasta, lemon, bread and orange. The second transaction (T2) indicates that a customer has bought pasta and lemon together. Transaction T3 indicates that a customer bought pasta, orange and cake, while transaction T4 indicates that someone bought pasta, lemon, orange with cake.

If we have such data, we can apply pattern mining algorithms to discover interesting pattern in it. Several algorithms are available for this. The traditional task is to find the frequent itemset mining, that is all the sets of items (itemsets) that appear more than minsup times in a database, where minsup is a threshold set by the user. For example, if the user set minsup = 2, then the goal of frequent itemset mining is to find all sets of items that have been purchased at least twice by customers. For instance, in the above database, the frequent itemsets are the following:

For instance, {lemon} is said to be a frequent itemset because it appears at least twice in the database above. In fact, lemon actually appear three times (in transactions, T1, T2 and T4). Another example is the itemset {pasta, cake}, which is said to be frequent because it appears in two transactions (T3 and T4). Generally, if an itemset appears in X transactions, we say that an itemset has a support of X transactions. For instance, we say that the itemset {lemon} has a support of 3 and the itemset {pasta, cake} has a support of 2. If we want to visualize the frequent itemsets and all the possible itemsets, we can draw a picture called a Hasse Diagram, shown below:

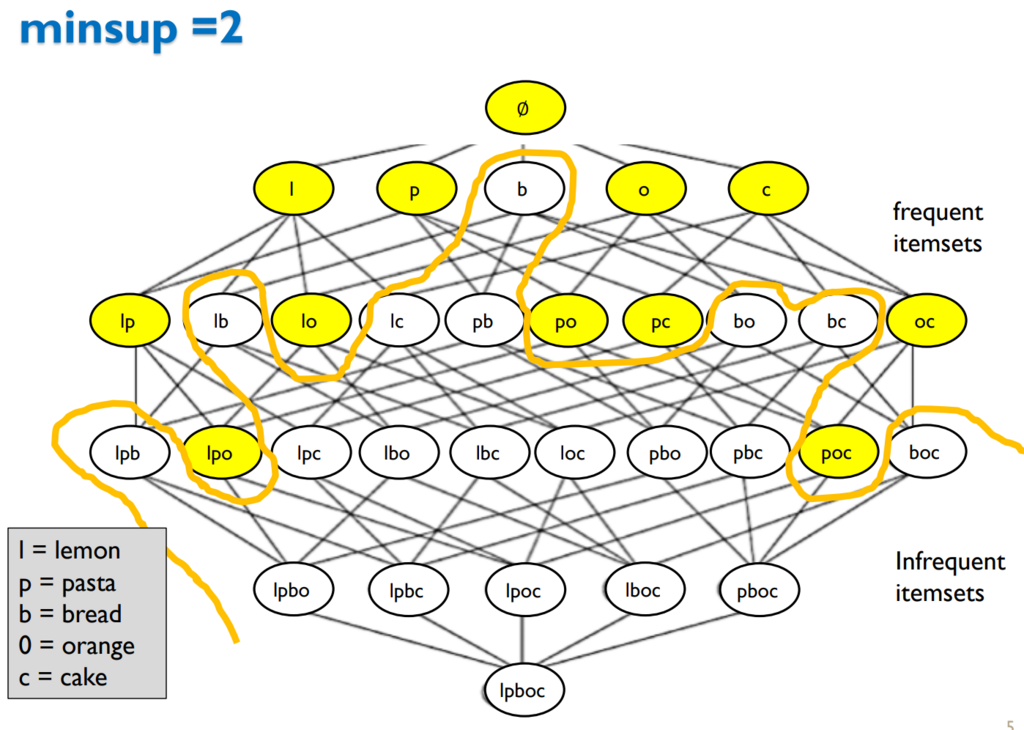
In this picture, we have all the possible itemsets (combinations of items) that customers could buy together. To make the picture easier to read, we use the letters l, p, b, o, c to represents the items lemon, pasta, bread, orange, and cake, respectively. So for example, the notation “poc” means to buy pasta, orange and cake together. In the picture, the frequent itemsets are colored in yellow, while the infrequent itemsets are colored in white. And there is an edge between two itemsets if one is included in the other and the other has one more item. For example, there is an edge from “po” to “poc” because “po” is included in “poc” and “poc” has one more item. Totally, if we have five items such as in this case, there is a total of 2^5 = 32 possible itemsets, as depicted in this picture. The itemset on top of this picture is the empty set, while the one at the bottom is “lpboc”, which means to buy all the five items together.The problem of frequent itemset mining thus aims at finding values that appear frequently together (the yellow itemsets0. But what if we want to find the itemsets that are rare instead of frequent? To do this, we first need to define what we mean by rare itemset. There are a few definitions. I will give a brief overview.

Definition 1: the infrequent itemsets

The most intuitive definition of what is a rare itemset is that it is an itemset that is not frequent. Thus, we can say that a rare itemset is an itemset that has a support that is less than the minsup threshold set by the user. Formally, we can write that an itemset X is infrequent if sup(X) < minsup, where sup(X) represents the support of X.

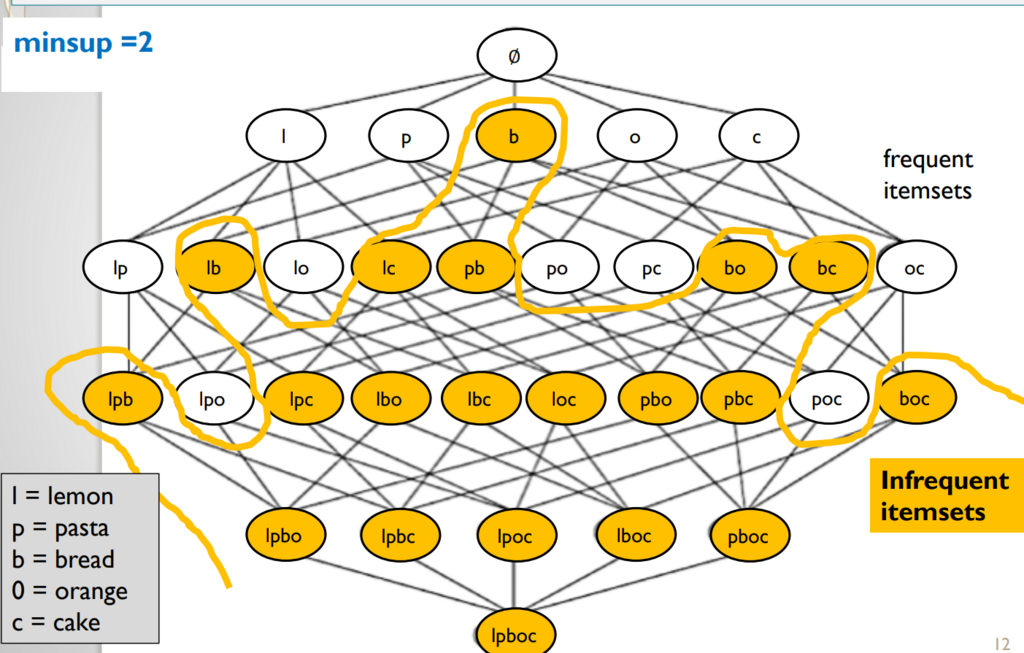
For example, if minsup = 2, the infrequent itemsets are illustrated in orange color in the picture below:

All these itemsets are infrequent because their support is less than 2. For example the itemset “bo” (bread and orange) has a support of 1, while “bc” (bread and cake) has a support of 0.Is this a good definition? No, because there are just too many infrequent itemsets. And in fact, it can be observed that many of them never appear in the database. For example, “pboc” (pasta, bread, orange and cake) is an infrequent pattern, but it has a support of zero because no customer has bought these items together. It is obviously uninteresting to find such patterns that have a support of zero. Itemsets having a support of zero are illustrated with a X in the picture below:

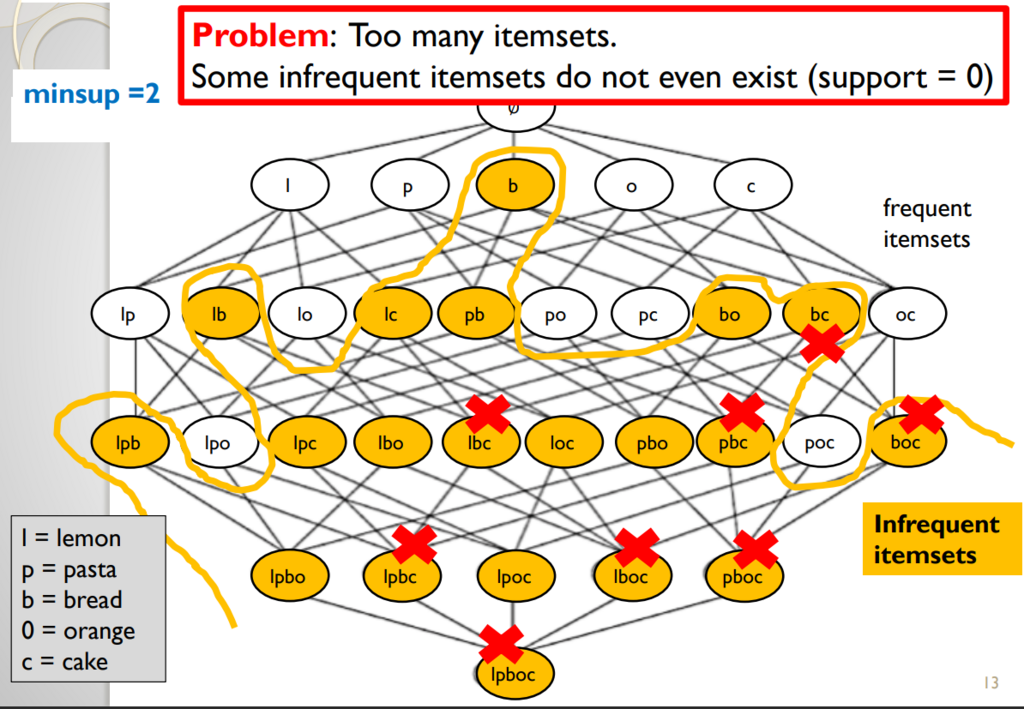
Thus, we may try to find a better definition of what is a rare itemset so that we will not find too many rare itemsets.

Definition 2: minimal rare itemsets

An alternative definition of what is a rare itemsets was proposed. An itemset X is said to be a minimal rare itemset if sup(X) <= minsup and all (proper) subsets of X are frequent itemsets. To make this easier to understand, I have illustrated the minimal rare itemsets on the picture below for minsup = 2 for the same example.

Here we can see that there are only two minimal rare itemsets, which are “lc” and “b”. “lc” is a minimal rare itemset because its support is less than 2, and all its subsets (“l” and “c”) are frequent. And “b” is a minimal rare itemset its suport is less than 2 and all its subsets are frequent (in this case, the only subset of “b” is the empty set, which is always frequent by definition).

Thus, if we find only the minimal rare itemsets, we may find a small set of itemsets that are almost frequent.

The first algorithm that was proposed to find minimal rare itemsets is AprioriRare by Szathmary & al (2007) in this paper:

Laszlo Szathmary, Amedeo Napoli, PetkoValtchev:Towards Rare Itemset Mining. ICTAI (1) 2007: 305-312

An efficient open-source implementation of AprioriRare can be found in the SPMF software.

Definition 3: perfectly rare itemsets

Another definition of what is a rare itemset was proposed by Koh et al. (PAKDD 2005). They define the concept of perfectly rare itemset as follows:

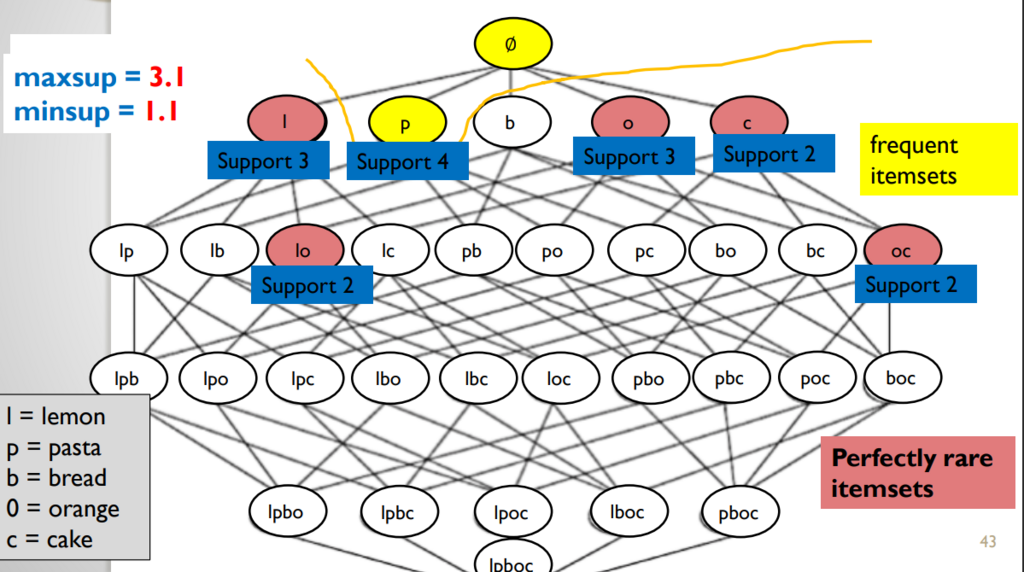
In that definition, the key idea is to use two threshold minsup and maxsup. Then, the aim is to find all itemsets that have a support no less than minsup and contain items with a support less than maxsup.

To show and example, of the type of results that this provides, here is the perfectly rare itemsets for minsup = 1 and maxsup = 1.9 for the same example:

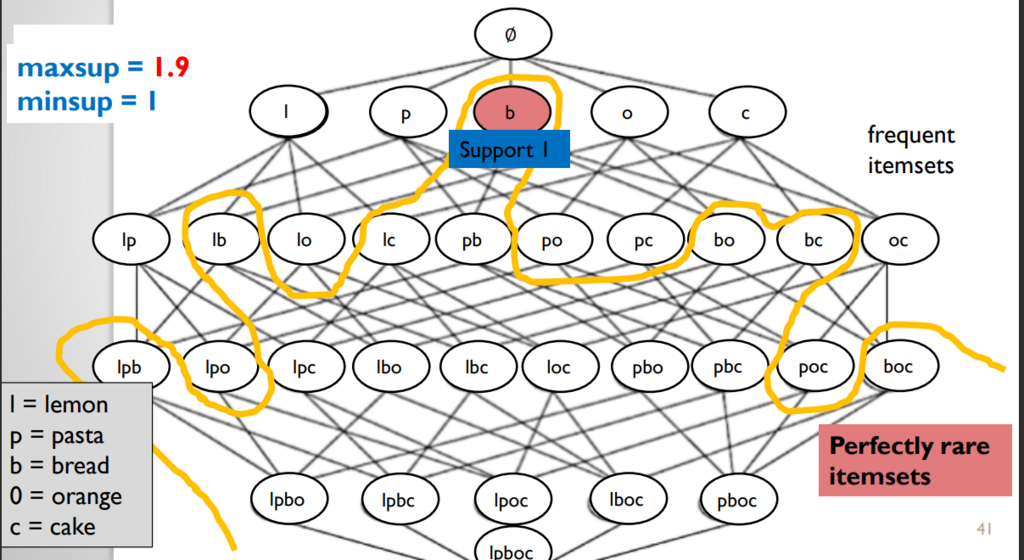
And if we change the parameters a little bit, here is the result:

The first algorithm for mining perfectly rare itemset is AprioriInverse by Koh et al. in this paper:

Yun Sing Koh, Nathan Rountree: Finding Sporadic Rules Using AprioriInverse. PAKDD 2005: 97-106

An open-source implementation of AprioriInverse can be found in the SPMF software.

Other extensions

There also exist other extensions and variations of the problem of rare itemset mining besides what I have covered in this blog post. My aim was to give a brief overview.

Software for rare itemset mining

If you want to try rare itemset mining, you can check the SPMF software, as I have mentioned above. It provides over 250 algorithms for various pattern mining tasks, including several algorithms for rare pattern mining. SPMF is written in Java but can be called from various languages and use also as a standalone application.

A video lecture on rare itemset mining

If you want to know more about the topic of rare itemset mining, you can also watch my video lecture on this topic, which is part of my free online course about pattern mining.

Conclusion

In this blog post, I have explained briefly what is rare itemset mining, that is how to find infrequent patterns in data. I mainly explained the different problem definitions but did not go into details about how the algorithms work to keep the blog post short. Hope you have enjoyed this. If you have any questions or feedback, please leave a comment below. Thank you for reading!

By the way, if you are new to itemset mining, you might be interested to check these two survey papers that give a good introduction to the topic:

• Fournier-Viger, P., Lin, J. C.-W., Vo, B, Chi, T.T., Zhang, J., Le, H. B. (2017). A Survey of Itemset Mining. WIREs Data Mining and Knowledge Discovery, Wiley, e1207 doi: 10.1002/widm.1207, 18 pages.
• Luna, J. M., Fournier-Viger, P., Ventura, S. (2019). Frequent Itemset Mining: a 25 Years Review. WIREs Data Mining and Knowledge Discovery, Wiley, 9(6):e1329. DOI: 10.1002/widm.1329

—
Philippe Fournier-Viger is a professor of Computer Science and also the founder of the open-source data mining software SPMF, offering more than 250 data mining alg