What is a maximal itemset?

In data mining, an itemset is a collection of items that occur together in a transactional dataset. For example, if we have a dataset of customer purchases, an itemset could be {bread, cake, orange}, meaning that these three items were bought together by several customers.

A frequent itemset is an itemset that occurs at least a certain number of times (or percentage) in the dataset. This number or percentage is called the minimum support threshold and it is usually specified by the user (but could be set automatically). For example, if we set the minimum support threshold to 3, then {bread, milk, eggs} is a frequent itemset if it occurs in 3 or more transactions in the dataset.

A maximal frequent itemset is a frequent itemset for which none of its immediate supersets are frequent. An immediate superset of an itemset is an itemset that contains one more item than the original itemset. For example, {bread, cake, orange, pasta} is an immediate superset of {break, cake, orange}. A maximal frequent itemset is thus a frequent itemset that cannot be extended with any other item without losing its frequency.

To illustrate this concept, consider the following example:

Transaction ID	Items
1	A B C D
2	A B D
3	A C D
4	B C D

Assume that the minimum support threshold is 50%, meaning that an itemset must occur in at least 2 transactions to be frequent (since this datasets has four transactions). The following table shows all the possible itemsets and their support counts (number of transactions in which they occur):

Itemset	Support count (how many times an itemset appears in the database)
A	3
B	3
C	3
D	3
AB	2
AC	2
AD	3
BC	2
BD	3
CD	3
ABC	1
ABD	2
ACD	2
BCD	2
ABCD	1

Based on the minimum support threshold, the frequent itemsets are A, B, C, D, AB, AC, AD, BC, BD, CD, ABD, ACD, and BCD. Out of these 13 frequent itemsets, only three are identified as maximal frequent: ABD, ACD and BCD. This is because none of their immediate supersets (ABCD) are frequent. The remaining frequent itemsets are not maximal frequent because they all have at least one immediate superset that is frequent. For example, B is not maximal frequent because AB, BC and BD are all frequent.

Why are maximal frequent itemsets useful?

Maximal frequent itemsets provide a compact representation of all the frequent itemsets for a given dataset and minimum support threshold. This is because every frequent itemset is a subset of some maximal frequent itemset. For example, in the above example, all the frequent itemsets are subsets of either ABD, ACD or BCD. Therefore, by knowing ABD, ACD and BCD and their support count, we can derive all the other frequent itemsets but we many not know their exact support count.

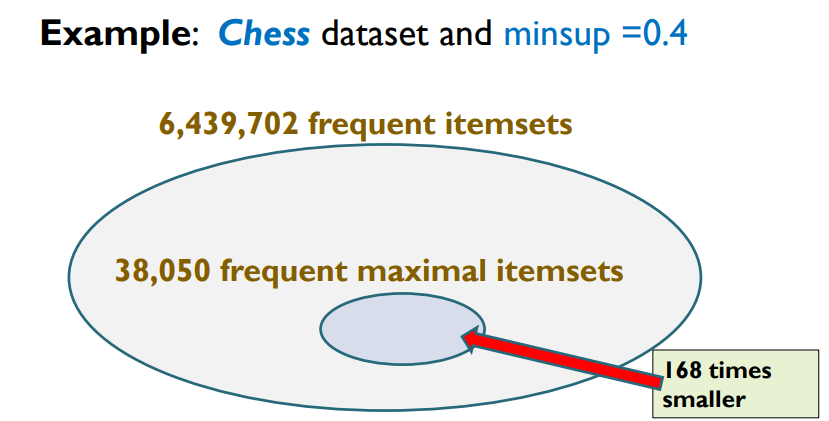
It is useful to discover maximal frequent itemsets because it gives a summary of all frequent itemsets to the user. Also discovering maximal frequent itemsets can be faster and require less memory and storage space than finding all the frequent itemsets. I will give an example of a real benchmark dataset called Chess to show how compact the maximal itemsets can be. If we set minsup = 40% on Chess, we get about 6 millions frequent itemsets but only 38,050 maximal frequent itemsets.

Note that besides maximal itemsets there also exists other compact representations of frequent itemsets such as closed itemsets and generator itemsets.

How to find maximal frequent itemsets?

There are several algorithms for finding maximal frequent itemsets from a transactional dataset. They are generally variations of the popular frequent itemset mining algorithm such as FPGrowth, Eclat and Apriori.

One of the most efficient algorithm for maximal itemset is FPMax, which is based on the FP-Growth algorithm. It uses a compact data structure called FP-tree. FPMax builds an FP-tree from the dataset and then mines it recursively by generating conditional FP-trees for each item. It uses several pruning strategies to avoid generating non-maximal frequent itemsets and reduce the size of the conditional FP-trees.

Some other notable algorithms for maximal itemset mining are MAFIA, LCM_MAX and GENMAX.

Source code and datasets

If you want to try discovering frequent itemsets, closed itemsets, maximal itemsets and generator, you can check the SPMF data mining software, which is implemented in Java and can be called from other popular programming languages as well. It is highly efficient an open-source, with many examples and datasets.

Video

If you are interested to learn more about this topic, you can also watch a 50 minute video lecture where I explain in more details what are maximal itemsets, closed itemsets and generator itemsets. This video is part of my free pattern mining course, and you can watch from my website here: Maximal, Closed and Generator itemsets or from my youtube channel here

Conclusion

In this blog post, I have explained briefly what is a maximal itemset, why it is useful, and talked about some algorithms for this problem. Hope that you have enjoyed this post!

By the way, if you are new to itemset mining, you might also be interested to check these two survey papers that give a good introduction to the topic:

• Fournier-Viger, P., Lin, J. C.-W., Vo, B, Chi, T.T., Zhang, J., Le, H. B. (2017). A Survey of Itemset Mining. WIREs Data Mining and Knowledge Discovery, Wiley, e1207 doi: 10.1002/widm.1207, 18 pages.
• Luna, J. M., Fournier-Viger, P., Ventura, S. (2019). Frequent Itemset Mining: a 25 Years Review. WIREs Data Mining and Knowledge Discovery, Wiley, 9(6):e1329. DOI: 10.1002/widm.1329

—
Philippe Fournier-Viger is a professor of Computer Science and also the founder of the open-source data mining software SPMF, offering more than 250 data mining algorithms.