In this blog post, I will explain why the FSMS algorithm for frequent subgraph mining is an incorrect algorithm. I will publish this blog post because I have found that the algorithm is incorrect after spending a few days to implement the algorithm in 2017 and wish to save time to other researchers who may also want to implement this algorithm.
This post will assume that the reader is familiar with the FSMS algorithm, published in the proceedings of the Industrial Conference on Data Mining.
Abedijaberi A, Leopold J. (2016) FSMS: A Frequent Subgraph Mining Algorithm Using Mapping Set, Proceedings of the 16th Industrial Conference on Data Mining (Ind. CDM 2016). Springer, 2016: 761-773.
I will first give a short summary of why the algorithm is incorrect and then give a detailled example to illustrate the problem.
Brief summary of the problem
The FSMS algorithm creates some mapping sets. The purpose of a mapping set is to keep track of vertices that are isomorphic for different subgraph instances. But I have found that in some cases we can expand a subgraph instance from two different vertices that are not isomorphic according to the mapping set but that will still generate some graph instances that are isomorphic. The problem that occurs is that FSMS does not detect that these graph instances are isomorphic using the mapping sets.
Thus, the support of subgraphs may be incorrectly calculated and some frequent subgraphs may be missing from the output of the algorithm.
Example
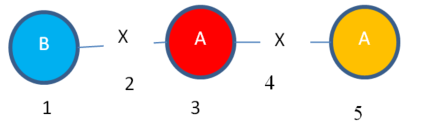
The above short description may not be clear. So let me explain this now with an example. Consider that we have the following graph with five vertices and two edges. The vertex labels are A, B and the edge label is X. The numbers 1,2,3,4,5…9 are some ids that I will use for the purpose of explanation.

In the above graph, I can find various subgraphs. Consider the following subgraph that I will call “Subgraph1”:
Subgraph1:
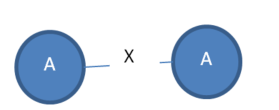
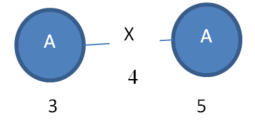
The subgraph “Subgraph1” has two instances:
Instance 1:
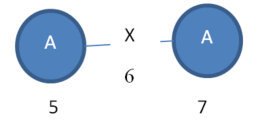
Instance 2:
Moreover, we can say that “Subgraph 1” has a support of 2.
We can also say that “Subgraph 1” has the following values:
VALUES 3-4-5
VALUES 5-6-7
and the following mapping set:
A = 3,5
A = 5,7
Just to make my example easier to understand, we can visualize these mapping set entries of “Subgraph 1” using colors. We have two entries. One is RED. The other one is ORANGE.
Instance 1:
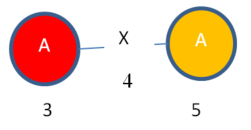
Instance 2:
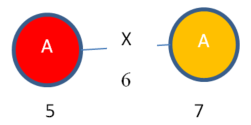
Ok, so we have a subgraph called “Subgraph 1” and we have its mapping set. Now, let’s continue my example. We will expand our subgraph “Subgraph 1” to find larger subgraph(s). According to the FSMS algorithm, we should find the edges that extend each mapping set entry (each color), as we know that this will generate some subgraphs that are isomorphic.
So, I can expand vertex 3 of “Instance 1” to obtain this subgraph instance:
Instance 4:
Moreover, I can expand vertex 7 of “Instance 2” to obtain this subgraph instance:
Instance 5:
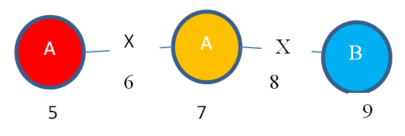
Obviously, “Instance 4” and “Instance 5” are isomorphic.
But the problem that I have found is that these two instances are not obtained by expanding the same entries in the mapping sets of “Subgraph 1”. To obtain “Instance 4” I have expanded the RED entry of the mapping set (vertex 3). But to obtain “Instance 5”, I have expanded the ORANGE entry of the mapping set (vertex 7). But the resulting instances (“Instance 4” and “Instance 5”) are isomorphic.
Thus the FSMS algorithm is unable to detect that these two instances (“Instance 4” and “Instance 5”) are isomorphic.
If these two instances had been obtained by expanding vertices from the same mapping set entry (color) of “Subgraph1”, we would know that “Instance 4” and “Instance 5” are isomorphic. But in my example, these two instances are not obtained by extending the same entry of the mapping set of “Subgraph 1”.
When this problem occurs?
My above example is very simple. But the same problem can happen for larger subgraphs with more edges. In general, how can we detect that extending different entries (colors) of a mapping set yield isomorphic graph instances? Actually, this problem only occurs if we have many nodes with the same label. If we do not have many nodes with the same labels, it will not happen. But we still need to deal with this problem since in real-life a graph may have multiple vertices with the same labels.
Can this problem be fixed?
There does not seem to be a simple solution to fix the problem. Actually, one may think that a solution is to perform isomorphic tests. But the FSMS algorithm was designed to avoid isomorphic tests. Thus, it would defeat the purpose of the algorithm. I have thought about it for a while but did not find any simple solution to fix the algorithm.
Conclusion
In this blog post, I have reported a problem in the FSMS algorithm such that the result is incorrect. I have actually implemented the algorithm and tested it extensively, which has led to finding this issue. If someone is interested in obtaining the Java implementation of the algorithm that I have made, I could share it by e-mail.
The other conclusion that can be made is that it is easy to overlook some cases when designing and algorithm. There are actually several published algorithms that contain errors, even in top conferences/journals. For researchers, a solution to avoid such issue is to always provide a proof of correctedness/completedness, and to extensively test an implementation for bugs.
==
Philippe Fournier-Viger is a full professor and the founder of the open-source data mining software SPMF, offering more than 110 data mining algorithms. If you like this blog, you can tweet about it and/or subscribe to my twitter account @philfv to get notified about new posts.






Hi, I am final year students. I am interested in obtaining the Java implementation of the FSMS algorithm. You can share it by my e-mail nguyenchicongmta@gmail.com. Thank you very much!
I have sent the code to your e-mail yesterday 😉