Brief report about the IEA AIE 2021 conference

Posted on 2021-07-26 by Philippe Fournier-Viger

This week, it is the IEA AIE 2021 conference (34th Intern. Conf. on Industrial, Engineering & Other Applications of Applied Intelligent Systems), which is held from 26th to 28th June 2021. This year, the conference is held online due to the COVID pandemic situation around the world.

In this blog post, I will give an overview of the conference.

About IEA AIE 2021

The IEA AIE conference is a conference that focuses on artificial intelligence and its applications. I have attended this conference several times over the year. I have written some blog posts also about IEA AIE 2016, IEA AIE 2018, IEA AIE 2019 and IEA AIE 2020.

This year, there has been 145 papers submitted. From this, 87 papers were accepted as full papers, and 19 as short papers.

Special sessions

This year, there was eight special sessions organized at IEA AIE on some emerging topics. A special session is a special track for submitting papers, organized by some guest researchers. All accepted papers from special sessions are published in the same proceedings as regular papers.

  • Special Session on Data Stream Mining: Algorithms and Applications
  • (DSMAA2021)
  • Special Session on Intelligent Knowledge Engineering in Decision Making Systems
  • (IKEDS2021)
  • Special Session on Knowledge Graphs in Digitalization Era (KGDE2021)
  • Special Session on Spatiotemporal Big Data Analytics (SBDA2021)
  • Special Session on Big Data and Intelligence Fusion Analytics (BDIFA2021)
  • Special Session on AI in Healthcare (AIH2021)
  • Special Session on Intelligent Systems and e-Applications (iSeA2021)
  • Special Session on Collective Intelligence in Social Media (CISM2021).

Opening ceremony

On the first day, there was the opening ceremony. It was announced that IEA AIE 2022 will be held in Japan next year.

Keynote speakers

There was two keynote speakers: (1) Prof. Vincent Tseng from National Yang Ming Chiao Tung University, (2) Prof. Francisco Herrera from University of Granada.

Paper presentations

I have attended several paper presentations through the conference. There was some high quality papers on various topics related to artificial intelligence. There was four rooms with paper presentations. Here is a screenshot of one of the rooms:

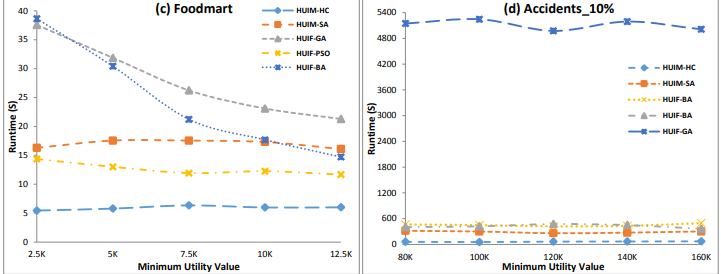
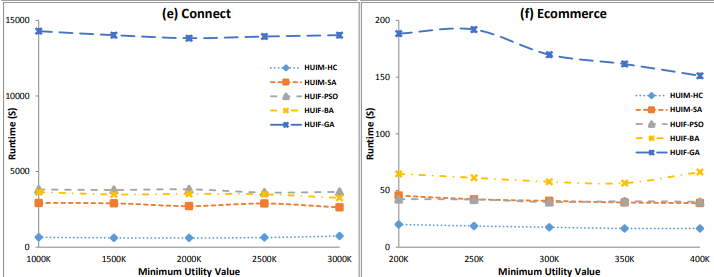
In particular, this year, there was six papers on pattern mining topics such as high utility pattern mining, sequential pattern mining and periodic pattern mining:

  • Oualid Ouarem, Farid Nouioua, Philippe Fournier-Viger: Mining Episode Rules from Event Sequences Under Non-overlapping Frequency. 73-85
    Comment: This paper presents a novel algorithm for episode rule mining called NONEPI. The idea is to find rules using the non-overlapping frequency in a sequence of events.
  • Sumalatha Saleti, Jaya Lakshmi Tangirala, Thirumalaisamy Ragunathan: Distributed Mining of High Utility Time Interval Sequential Patterns with Multiple Minimum Utility Thresholds. 86-97
    Comment: This paper presents a new algorithm DHUTISP-MMU for mining high utility time interval sequential patterns with multiple minimum utility thresholds. A key idea in this paper is to add information about the time intervals between items of sequential patterns. Besides, the algorithm is distributed.
  • Xiangyu Liu, Xinzheng Niu, Jieliang Kuang, Shenghan Yang, Pengpeng Liu: Fast Mining of Top-k Frequent Balanced Association Rules. 3-14
    Comment: This paper presents an algorithm named TFBRM for mining the top-k balanced association rules. There has been a few algorithms for top-k association rule mining in the bast. But here a novelty is to combine support, kulczynski (kulc) and imbalance ratio (IR) as measures to find balanced rules.
  • Penugonda Ravikumar, Likhitha Palla, Rage Uday Kiran, Yutaka Watanobe, Koji Zettsu: Towards Efficient Discovery of Periodic-Frequent Patterns in Columnar Temporal Databases. 28-40
    Comment: This paper presents an Eclat-based algorithm for periodic pattern mining called PF-Eclat. From the presentation it seems to me that this algorithm is very similar to the PFPM algorithm (2016) that I proposed 5 years ago. The difference seems to be that the vertical representation is a list of timestamps instead of list of TIDs, and it has two less constraints. That is the user can only use maxPer and minSup(minAvg) as constraints but PFPM also offers two more constraints: minPer and maxAvg. By the way, there exists also another Eclat based algorithm for a similar task (mining top-k periodic frequent patterns) called MTKPP (2009).
  • Sai Chithra Bommisetty, Penugonda Ravikumar, Rage Uday Kiran, Minh-Son Dao, Koji Zettsu: Discovering Spatial High Utility Itemsets in High-Dimensional Spatiotemporal Databases. 53-65
  • Tzung-Pei Hong, Meng-Ping Ku, Hsiu-Wei Chiu, Wei-Ming Huang, Shu-Min Li, Jerry Chun-Wei Lin: A Single-Stage Tree-Structure-Based Approach to Determine Fuzzy Average-Utility Itemsets. 66-72
    Comment: This paper is about fuzzy high utility itemset mining. A novel algorithm is presented. A difference also with previous paper is the use of the average utility function in fuzzy high utility itemset mining.

Next year

The IEA AIE 2022 conference will be held in Kitakyushu, Japan.

Conclusion

This was a good conference. I have attended several presentations and had a chance to discuss with some interesting researchers. Looking forward to the IEA AIE 2022 conference.

Philippe Fournier-Viger is a full professor working in China and founder of the SPMF open source data mining software.

Related posts:

PAKDD 2018 Conference (a brief report)
Brief report about the IEA AIE 2016 conference
Brief report about the ECML PKDD 2021 conference
Posted in artificial intelligence, Conference, Machine Learning | Tagged , , , , , , | 7 Comments

Brief report about the DSIT 2021 conference (4th Intern. Conf. on Data Science and Information Technology)

Posted on 2021-07-23 by Philippe Fournier-Viger

This week, I am attending the DSIT 2021 conference (4th International Conference on Data Science and Information Technology) from July 23 to 25 in Shanghai, China.

The DSIT 2021 conference is co-located with the DMBD 2021 conference (the 4th International Conference on Data Mining and Big Data).

DSIT is a relatively young conference, which focuses on data science and data mining. But the quality was good and it was well organized. The proceedings of the conference are published by ACM. Thus, all papers are in the ACM Digital Library. This gives visibility to the papers.

A total of 150 submissions were received and 80 full papers were accepted for publication (acceptance rate = 53%). The papers were from several countries including China, Japan, Singapore, Vietnam, Philippines, Pakistan, Thailand, USA, Greece, France and Germany.

There was also several keynote speakers: Prof. Tok Wang Ling from National University of Singapore, Prof. Ma Maode from Nanyang Techn. University of Singapore, Prof. Shigeo Akashi from Tokyo University of Science, Japan and Prof. Philippe Fournier-Viger (myself) from Harbin Inst. of Technology (Shenzhen), China.

Due to the COVID pandemic and travel restrictions, the conference was held in Shanghai but some speakers were online through Zoom.

Day 1 – Registration

On the first day, I registered at the conference reception desk at hotel and receive a bag with the program, ID card, a small gift, and other things.

Day 2 – Keynote Talk

First, there was the opening ceremony.

Then, it was the keynote talks. I started first with my invited talk on algorithms for discovering patterns in data that are in interpretable (pattern mining).

Then, there was the talk by Prof. Jie Yang on adversarial attacks on deep neural networks. He has shown some recent work on generating adversarial pictures to fool neural networks. For instance a picture of a car may be slightly modified to fool a neural network into believing it is a house. What I find the most interesting about this talk is that it was shown that some modified pictures can fool not only one network but all the state of the art deep neural networks for image recognition. The reason why it is possible to fool multiple networks with a same modified picture is that an attack based on attention was used and that many deep neural networks will use attention in a similar way (focusing on the same image features). A dataset of adversarial images called DAmageNet was also presented, which can be helpful to test ways to protecting against such attacks. An interesting conclusion was that these attacks are possible because deep neural models tend to ignore some important features and incorporate unnecessary features.

adversarial attack deep learning
DAmageNet attention attack
database of adversarial examples
deep learning attack

Then, there was the other keynote talks.

Day 2 – Paper presentation

Then there was the regular paper presentations and a poster session.

There was two papers related to pattern mining. The first one was about high utility itemset mining and the other about frequent pattern mining.

  • High Utility pattern mining based on historical data table over data streams by Xinru Chen, Pengjun Zhai and Yu Fang
  • MaxRI: A method for discovering maximal rare itemsets by Sadeq Darrab et al.

I took some pictures of a few slides from that paper about maximal rare itemsets, as I find this to be an interesting topic:

Conclusion

This is all I will write for this conference. Overall, that was an interesting conference. It is not a very big conference but I met some other interesting researchers and we had some good discussions. Some papers were also quite good.

In a few days, I will be attending the IEA AIE 2021 conference and will report also about it.

—

Philippe Fournier-Viger is a full professor working in China and founder of the SPMF open source data mining software.

Related posts:

Towards SPMF v3.0...
This is why you should visualize your data!
SPMF’s architecture (4) The MemoryLogger
Posted in artificial intelligence, Big data, Conference, Data Mining | Tagged , , , , , , , | 2 Comments

Brief report about the CCF-AI 2021 conference

Posted on 2021-07-21 by Philippe Fournier-Viger

This week, I attend the CCF-AI 2021 conference, which is the Chinese Computer Federation conference on Artificial Intelligence. This conference is held in the city of Yantai (烟台) in Shandong province of China, from the 22th to 24th July 2021.

About CCF-AI

CCF-AI is a national conference. But it is a major conference in China, with over 1,000 attendees. I attend this conference to meet other researchers and get to know about the recent results in this area. There are many high level speakers at the conference and activities.

In the past CCF-AI has been held in various locations around China. Here is a few of them:

Location

The city where CCF-AI is held this year is Yantai (烟台). It is a coastal city in eastern China, in Shandong province. It has good weather during the summer, beaches and many other activities.

The conference was held at the Yantai International Expo Center:

Registration

After arriving at the hotel, all attendees have to pass a test for the COVID to ensure the safety of everyone at the conference. Then, I registered and received my bag and badge with the program and other information.

Day 1 – Multi-Agent Systems forum

The conference is divided into some sub-forums. On the morning of the first day, I attended the multi-agent system forum. I also had some good discussions with other researchers.

Day 1 – Meeting of CCF-AI members

On the evening, I attended the meeting of CCF-AI members.

It was voted that CCF-AI 2023 will be held at Xinjiang University in Urumqi, China.

There was also a vote to select new members of CCF-AI. I am happy to have been selected:

It was said that for CCF–AI 2021, 339 papers were submitted and 128 papers were accepted (38% acceptance rate).

Other days and conclusion

There was also many other interesting activities and talks at this conference in the following days. However, my schedule was very tight. I came to CCF-AI, right after attending ICSI 2021, and I had to leave on the second day of CCF-AI to go to Shanghai to attend the DSIT 2021 conference in Shanghai, which I will talk about in the next blog post! Then, I will also attend the IEA AIE 2021 conference.

—

Philippe Fournier-Viger is a full professor working in China and founder of the SPMF open source data mining software.

Related posts:

Brief report about the IEA AIE 2021 conference
Expensive Academic Conferences – the case of ICDM
The PAKDD 2020 conference (a brief report)
Posted in artificial intelligence, Conference, Machine Learning | Tagged , , , , , , , , , , | 1 Comment

Brief report about ICSI 2021 (12th Int. Conference on Swarm Intelligence)

Posted on 2021-07-15 by Philippe Fournier-Viger

In this blog post, I will talk about attending the 12th International Conference on Swarm Intelligence (ICSI 2021). The ICSI conference is a relatively young conference about swarm intelligence, metaheuristics and related topics and applications. This year, ICSI 2021 is held in Qingdao, a coastal city in eastern China, from July 17–21, 2021. The conference is also held partially online for those that cannot attend due to travel restrictions.

The conference was held at the Blue Horizon Hotel:

The ICSI conference has been held in several cities and countries, over the years:

  • ICSI 2020 – Serbia (virtual)
  • ICSI 2019 – Chiang Mai, Vietnam
  • ICSI 2018 – Shanghai, China
  • ICSI 2017 – Fukuoka, Japan
  • ICSI 2016 – Bali, Indonesia
  • ICSI-CCI 2015 – Beijing, China
  • ICSI 2014 – Hefei, China
  • ICSI 2013 – Harbin, China
  • ICSI 2012 – Shenzhen, China
  • ICSI 2011 – Chongqing, China
  • ICSI 2010 – Beijing, China

Proceedings

The proceedings of the ICSI conference are published in the Springer Lecture Notes in Computer Science (LNCS) series as two volumes (Part 1 and Part 2). This ensures that the proceedings are indexed by EI and other indexes like DBLP.

ICSI conference proceedings (swarm intelligence)

This year, the conference received 177 submissions, which were reviewed on average by 2.5 reviewers. From this 104 papers were accepted for publications, which means an acceptance rate of 58.76%. The paper were organized into 16 sessions.

Day 1 – Registration

On the first day, I registered. I received a paper bag with a badge and the conference program. The proceedings was available online as a download.

Day 1 – Reception

There was also a reception at the hotel in the evening that lasted about an hour. There was food, beer and other drinks. This was a social activity, which is a good opportunity to discuss with other researchers that attend the conference.

Day – 2 – Opening ceremony
On the second day there was the opening ceremony, where the general chair talked about the conference, and the program.

The program committee chair also talked about the paper selection process.

Day – 2 – Keynote talks and invited talks

On the second day, there was two keynote talks and two invited talks. Some good researchers had been invited, and some of the talks were quite interesting. Below is a very brief overview.

The first keynote talk was by Prof. Qirong Tang from Tongji University who talked about “Large-Scale Heterogeneous Robotic Swarms”. He developed a swarm robotic platform that is used for some applications such as searching for multiple light sources, searching for a target, drug delivery in the body, etc. The idea is that some robots can cooperate together to perform a task more quickly (e.g. cooperative search) and thus outperform a single high quality robot. The swarm can be heterogeneous, that is using different types of robots such as flying robots and ground robots. Many bio-inspired algorithms are used to control a robot swarm such as particle swarm optimization (PSO) and genetic algorithms but it was argued that PSO is particularly suited for this task.

Some applications
Robots from a robot swarm

The second keynote talk was online by Prof. Chaomin Luo from USA about swarm intelligence applications to robotics and autonomous systems. This includes for example, exploration robots, search and rescue robots.

There was an invited talk by Prof. Gai-Ge Wang from Ocean university. He talked about how to improve the performance of metaheuristics using information feedback. The idea is that during iterations, some feedback of previous iterations is used to guide the search process towards better solutions.

The second invited talk was by Prof. Wenjian Luo from Harbin Institute of Technology (Shenzhen) about many-objectives optimization when multiple parties are involved. For example, to buy a car, many objectives may have to be considered such as the price, size, and fuel consumption and multiple parties such as an husband and wife may put different weights on those objectives. The goal is to find a solution that is optimal for all the parties involved but it is not always possible.

Day 2 – Paper presentations

On the afternoon, there was paper presentations and a poster session. There was some good papers about a variety of topics such as sheep optimization, classification of imbalanced data with PSO, citation analysis, swarm intelligence for UAVs, and multi-robot cooperation.

I have presented the below data mining paper about proof searching for proving theorems using simulated anneealing (which is mainly the work of my post-doc. M. S. Nawaz). In that paper, we use the simulated annealing metaheuristic to search for proofs to PVS theorems and compare with a genetic algorithm.

Nawaz, M. S., Sun, M., Fournier-Viger, P. (2021). Proof Searching in PVS theorem prover using Simulated Annealing. Proceedings of the 12th Intern. Conf. on Swarm Intelligence (ICSI 2021) Part II, pp. 253-262 

There was also a good paper by Prof. Wei Song et al. about using fish swarm optimization for high utility itemset mining:

Song, W. Li, J. Huang, C.: Artificial Fish Swarm Algorithm for Mining High Utility Itemsets. ICSI (2) 2021: 407-419

Day 2 – Banquet

In the evening, there was a banquet. The best paper awards were announced.

ICSI 2022
It was announced that next year the ICSI 2022 conference will be held in Xian, China from July 15 to 19 2022.

icsi 2022 swarm intelligence conference

Conclusion
Swarm intelligence is not my main research area although I have participated to several papers on this topic. But the conference was interesting and well organized. The quality was generally good. I would attend it again if I have some papers on this topic.

Now, I will leave Qingdao, and next I will attend the CCF-AI 2021 conference, DSIT 2021 conference, and then the IEA AIE 2021 conference.

—
Philippe Fournier-Viger is a professor of Computer Science and also the founder of the open-source data mining software SPMF, offering more than 120 data mining algorithms.

Related posts:

Brief report about the CACML 2022 conference
Brief report about the ECML PKDD 2021 conference
MLiSE 2021 @ PKDD 2021 - a new workshop!
Posted in artificial intelligence, Conference, Data Mining, Data science | Tagged , , , , , , , , , | 2 Comments

SPMF 2.48

Posted on 2021-06-28 by Philippe Fournier-Viger

Hi all, I have not been very active on the blog during the last month. This is because I had many thinsg going on in my personal and professional life that I will not reveal here. But I will be back soon with more regular content for the blog. Today, I write a blog post to give you some news:

SPMF 2.48

First, I would like to say that a new version of SPMF data mining software has just been released (v. 2.48) with two new algorithms:
– NEclatClosed  for mining closed itemsets
– HUIM-SPSO for mining high utility itemsets using Set-based Particle Swarm Optimization
Those are the original implementations, provided by the authors.

T com.

MLiSE 2021 – deadline extension

Third, I would like to mention that the deadline for submiting your papers to the MLiSE 2021 workshop at PKDD that I co-organize has been extended to the 15th July. The theme of the workshop is Machine Learning in Software Engineering but the scope can be more broad so if you have any question about the workshop, feel free to contact with me. I would be happy to see your paper 🙂

Conclusion

This blog post was just to give some quick update. Hope it has been interesting.

—
Philippe Fournier-Viger is a professor of Computer Science and also the founder of the open-source data mining software SPMF, offering more than 200 data mining algorithms.

Related posts:

SPMF’s architecture (3) The Preference Manager
The SPMF data mining library: a brief history and what's next?
An Overview of Pattern Mining Techniques
Posted in Machine Learning, Pattern Mining, spmf, Website | Tagged , , , , | Leave a comment

Brief report about ICIVIS 2021 (Int. Conference on Image, Vision and Intelligent system)

Posted on 2021-06-19 by Philippe Fournier-Viger

This week-end, I have attended the International Conference on Image, Vision and Intelligent system from 18 to 20 June 2021 in Changsha city, China.

It is a medium-sized conference (about 100 participants) but It is well-organized, and there was many interesting activites and speakers, as well as some workshops. The main theme of this conference is about image and computer vision but also some other works more related to intelligent systems where presented.

I have participated to this conference as an invited keynote speaker. I gave a talk on analyzing data for intelligent systems using pattern mining techniques. There was also an interesting keynote talk by Prof. Yang Xiao from University of Alabama, USA about detecting the theft of electricity from electricity networks and smart grids. Another keynote speaker was Prof. En Zhu from the National University of Defense Technology, who talked about detecting flow and anomalies in images. The fourth keynote speaker was Prof. Yong Wang from Central South University, about optimization algorithms and edge computing. That presentation has shown some cool applications such as drones being used to improve the internet coverage in some area or optimizing the placement of wind turbines in a wind farm. The last keynote speaker was Prof. Jian Yao from Wuhan University, about image-fusion. He shown many advanced techniques to transform images such as to fix light and stitching together overlaping videos.

This my pass, and program book:

Below, is the registration desk. The staff has been very helpful through the conference:

This is one of the room for listening to the talks:

This is a group picture:

There was also social activities such as an evening dinner and banquet, where I met many interesting researchers that I will keep contact with.

That is all of what I will write for today. It is just to give a quick overview of the conference. Next month, I will write about the ICSI 2021, CCF-AI 2021 , DSIT 2021 , and  IEA AIE 2021 conferences, that I will also attend.

—
Philippe Fournier-Viger is a professor of Computer Science and also the founder of the open-source data mining software SPMF, offering more than 120 data mining algorithms.

Related posts:

A brief report about the IEEE DSAA 2022 conference
UDML 2021 @ ICDM 2021
PAKDD 2018 Conference (a brief report)
Posted in Academia, artificial intelligence, Conference, Machine Learning | Tagged , , , , , , | Leave a comment

Key Papers about High Utility Itemset Mining

Posted on 2021-06-12 by Philippe Fournier-Viger

In this blog post, I will talk about the most important algorithms for high utility itemset mining. I will present a list of algorithms that is of course subjective (according to my opinion). I did not list all the papers of all authors but I have listed the key papers that I have read and found interesting, as they introduced some innovative ideas. This list is partly based on my survey of high utility itemset mining. To help you while reading these papers, you may also check my glossary of high utility itemset mining, which explain the key terms used in that research field.

Author / DatePaper titleKey idea
Yao 2004A Unified Framework for Utility-based Measures for Mining
Itemsets		– This paper defined the problem of high utility itemset mining.
Liu 2005A two-phase algorithm for fast discovery of high
utility itemsets		– The first complete algorithm for high utility itemset mining, named Two Phase.
– Two Phase is an Apriori based algorithm, and it does two phases to find high utility itemsets
– Introduced the TWU upper bound for reducing the search space.
Ahmed 2009Efficient Tree Structures for High-utility
Pattern Mining in Incremental Databases		– The first FP-Growth based algorithm for high utility itemset mining, named IHUP.
– Can discover high utility itemset incrementally.
Wu 2011 / 2013Efficient algorithms for mining high utility
itemsets from transactional databases		– Improved FP-Growth algorithms for high utility itemset mining, called UP-Growth and UP-Growth+.
– These algorithms adopt several strategies to reduce the TWU upper bound.
– The paper was published in KDD and then in TKDE, which gave a high visibility to high utility itemset mining.
Liu 2012Mining high utility itemsets without candidate generation– Presented HUI-Miner, the first algorithm for mining high utility itemset mining in one phase. This has revolutionized this field as all previous algorithms were using two phases. Speeds up of 10 to 100 times can be obtained compared to the previous best algorithms
– Introduced the remaining utility upper bound which is tighter than the TWU.
– HUI-Miner is based on Eclat
Fournier-Viger 2014FHM: Faster high-utility itemset mining
using estimated utility co-occurrence pruning		– Presented a fast vertical algorithm for high utility itemset mining, called FHM that adopts a new technique called co-occurrence pruning. This can further speed up the task by 5 to 10 times.
-FHM is based on HUI-Miner, and was shown to outperform it.
Fournier-Viger 2015 / 2016EFIM: A Highly Efficient
Algorithm for High-Utility Itemset Mining		– Another major performance improvement.
– This paper presented EFIM a novel algorithm that mines high utility itemsets almost in linear time and space.
– Introduced several new ideas for high utility mining like transaction merging and using arrays for utility and upper bound counting.
– The sub-tree utility upper bound can be tighter than the upper bounds of HUI-Miner and FHM.
– This algorihtm is inspired by HUI-Miner and LCM.
Duong 2017Efficient High Utility
Itemset Mining using Buffered Utility-Lists		– Proposed to reduce the memory usage of HUI-Miner and FHM based algorithms using the concept of buffered utility-lists.
– The modified algorithm is called ULB-Miner
Qu 2020Mining High Utility Itemsets Using Extended Chain Structure and Utility Machine– Proposed the REX algorithm, a one phase algorithm, which adopts new strategies such as k-item utility machine and a switch strategy.
Tseng 2013 /2015Efficient Algorithms for Mining Top-K High
Utility Itemsets		– Tseng proposed the task of top-k high utility itemset mining where the user directly set the number k of patterns to be found.
– In this journal version of the paper, a fast one-phase algorithm called TKO is presented, which extends HUI-Miner, and beat the TKU algorithm presented in the conference paper.
Fournier-Viger 2014Novel Concise Representations of High Utility
Itemsets using Generator Patterns		– To reduce redundancy, this paper proposed to discover a subsets of all high utility itemsets called the generators of high utility itemsets.
– An algorithm called GHUI-Miner is presented based on FHM.
– It can be argued that these itemsets are more useful in some case than all high utility itemsets.
Wu 2019Efficient algorithms for high utility
itemset mining without candidate generation		– This paper presented an algorithm called CHUI-Miner for discovering the maximal high utility itemset.
– This algorithm is based on HUI-Miner.
– Maximal itemsets are the largest one. Discovering them can greatly reduce the number of patterns shown to the user.
Fournier-Viger 2016FHM+: Faster High-Utility Itemset Mining using Length Upper-Bound Reduction– This paper makes the observation that finding very long patterns is unecessary.
-Thus an optimized algorithm called FHM+ is presented to reduce the upper-bounds and gain better performance when searching for high utility itemset using a length constraint.
– FHM+ is based on FHM
Fournier-Viger 2016PHM: Mining Periodic High-Utility
Itemsets		– This paper introduce the concept of periodic patterns in high utility itemset mining.
– The goal is not only to find patterns that have a high utility but also patterns that appear periodically over time. For example, one may find that a customer periodically purchase beer andwine every week or so.
– The PHM algorithm was presented, which is inspired by HUI-Miner and PFPM.
Wu 2015Mining Closed+ High Utility Itemsets
without Candidate Generation		– This is the first paper on closed high utility itemset mining.
– This paper introduced the CHUD algorithm, which is inspired by DCI_Closed.
– Closed itemsets allows to obtain a small set of high utility itemsets that provides concise information about all high utility itemsets (a summary).
– There have been several more efficient algorithms after that such as EFIM-Closed and CLS-Miner. However, CHUD is the first one.
Fournier-Viger 2015Mining Minimal High Utility Itemsets-This paper introduced a FHM-based algorithm called MinFHM to find the high utility itemsets that are minimal (not included in larger high utility itemsets).
– This can be useful for some applications.
Hong 2009Mining High Average-Utility Itemsets– This paper has introduced the problem of high average utility itemset mining.
– There has been many algorithms on this topic afterward. The utility is divided by the length of a pattern to avoid finding patterns that are too long.
– The TPAU and PBAU algorithms were presented which are inspired by Two-Phase, Apriori and Eclat.
Truong 2018Efficient Vertical Mining of High
Average-Utility Itemsets based on Novel Upper-Bounds		– This paper introduced the concept of vertical upper bounds in high average utility itemset mining. This has provided a major performance boost.
– The dHAUIM algorithm was presented, and published in TKDE, a top data mining journal.
Yin 2012USpan: an efficient algorithm for mining high utility sequential
patterns		– This paper presented an algorithm USpan for high utility sequential pattern mining, which is a related task that aims to find high utility patterns in sequence.
– It is not the first algorithm for this problem, but it was published in KDD and is arguably the most popular. Thus, I have selected it.
Lin 2015Mining high utility itemsets in big data– The first algorithm for mining high utility itemsets using a big data framework (Hadoop).
Zida 2015Efficient Mining of High
Utility Sequential Rules		– An algorithm named HUSRM to find high utility sequential rules.
– This topic is similar to high utility sequenital patterns mining but rules are found that have a high confidence.
Cagliero 2017Discovering high utility itemsets at multiple abstraction levels– The first paper to use a taxonomy of items for multi-level high utility itemset mining.
– The ML-HUI-Miner algorithm is an extension of HUI-Miner.
Fournier-Viger 2020Mining cross-level high utility itemsets– This paper has generalized the paper of Cagliero 2017 so as to find cross-level high utility itemsets (itemsets containing items from any abstraction levels of a taxonomy).
– The proposed CLH-Miner algorithm extends FHM. A top-k version of CLH-Miner called TKC was also proposed in another paper.
Chu et al., 2009An efficient algorithm for mining high utility itemsets with negative
item values in large databases		– Most algorithm for high utility itemset mining suppose that utility must be a positive number (e.g. amount of money).
– This is the first paper to consider that the utility can also be negative (e.g. selling an item at a loss in a supermarket).
– The HUI-NIV-Mine algorithm was designed for this task. It is a two phase algorithm inspired by Two-Phase.
Goyal 2015Efficient Skyline Itemsets Mining– This paper presented the first algorithm that mine skyline high utility itemsets.
– The idea is to find patterns that are not dominated by other patterns by considering their support and utility to find a Pareto front.
– Other more efficient algorithms were proposed later.
Nouioua 2021FHUQI-Miner: Fast High Utility Quantitative Itemset
Mining		– This paper presents the current state-of-the-art algorithm for high utility quantitative itemset mining.
– In this problem, patterns contains quantities. For example, a high utility itemset may say that a customer buys 2 to 5 breads with 1 or 2 bottles of milk.
– The original problem was proposed by Yen (2007) but this is the newest algorithm, based on FHM.
Kannimuthu1 2014Discovery Of High Utility Itemsets Using Genetic Algorithm With Ranked Mutation– This is one of the first heuristic algorithm for high utility itemset mining.
– It utilizes a genetic algorithm to find an approximation of all high utility itemsets.
– After that many algorithms have used other heuristics in recent papers.
Wu 2013Mining High Utility Episodes in Complex Event Sequences– Proposed US-Span, the first algorithm for finding high utility episodes, that is subsequences of high utility in a sequence of events.
Fournier-Viger, 2019HUE-SPAN: Fast High Utility Episode Mining.– Proposed a faster algorithm based on HUI-Miner, called HUE-SPAN for mining high utility episodes.
Fournier-Viger 2019Mining Local and Peak High Utility Itemsets– Proposed to consider the time dimension to find peak high utility itemsets and local high utility itemsets, that is itemsets that have a high utility in some non predefined time intervals (e.g. some products may yield a high product during Christmas time only).
– The LHUI-Miner algorithm and PHUI-Miner algorithm are variation of the FHM algorithm.
Fournier-Viger 2020Mining correlated high-utility itemsets using various measures– This paper aims to find correlated high utility itemsets, that is itemsets that not only have a high utility (importance) but also contains items that are highly correlated. This is to avoid finding patterns that have a high utility but just appear together by chance.
– Two measures from frequent itemset mining are incorporated into high utility itemset mining called the bond and all-confidence.
– The designed algorithm FCHM-Miner is an extension of the FHM algorithm.
…
…

Survey and videos

I wrote an easy to understand survey about high utility itemset mining, if you are interested by this topic, you may find it useful. Also, you may be interested in watching my video lectures on this topic on Youtube.

Conclusion

In this blog post, I have listed some key papers about high utility itemset mining. As I said above, this list is based on my opinion. But I think it can be useful. Hope you have enjoyed this post.

Philippe Fournier-Viger is a full professor working in China and founder of the SPMF open source data mining software.

Related posts:

How to run SPMF without installing Java?
The PrefixSpan algorithm (video)
(video) Rare Itemset Mining
Posted in Big data, Data Mining, Data science, Pattern Mining, Utility Mining | Tagged , , , , , , , | 1 Comment

Key Papers about Periodic Pattern Mining

Posted on 2021-05-20 by Philippe Fournier-Viger

In this blog post, I will list the key algorithms for periodic itemset mining (according to me) with comments about their contributions. Of course, this list is subjective. I did not list all the papers of all authors but I have listehttps://data-mining.philippe-fournier-viger.com/introduction-to-the-apriori-algorithm-with-java-code/d the key papers that I have read and found interesting, as they introduced some innovative ideas. I did not list papers that were mostly incremental in their contributions. I also did not list papers that had very few references unless I found them interesting.

AlgorithmAuthor / Date Key idea
PF-GrowthTanbeer 2009– First algorithm for periodic itemset mining in transactions
Uses the maxPer constraint to select periodic patterns.
– Based on FP-Growth
MTKPPAmphawan 2009– First algorithm for top-k periodic itemset mining
– Uses the maxPer constraint to select periodic patterns.
– Based on Eclat
ITL-treeAmphawan 2010– Performs an approximate calculation of the periods of patterns
– Based on FP-Growth
MIS-PF-tree Kiran 2009– Mining periodic patterns with a maxPer threshold for each item
– Based on FP-Growth
Lahiri 2010– Proposed to study periodic patterns as subgraphs in a sequence of graphs.
PFPRashid 2012– Find periodic itemsets using the variance of periods.
– The periodic patterns are called regular periodic patterns.
– Based on FP-Growth
PFPMFournier-Viger 2016– Generalize the problem of periodic itemset mining to provide more flexibility using three measures: the average periodicity, minimum periodicity and maximum periodicity
– It is shown that average periodicity is inversely related to the support measure.
– Based on Eclat
PHMFournier-Viger 2015– An extension of the PFPM algorithm to mine high utility itemsets (itemsets that are periodic but also important such as yield a high profit)
– Based on PFPM, Eclat and FHM
MPFPSFournier-Viger 2019
(ppt)		– Find periodic patterns in multiple sequences
– Introduce a measure called “sequence periodic ratio“
– Based on PFPM and Eclat
MRCPPSFournier-Viger 2019– Find periodic patterns in multiple sequences that are rare and correlated.
– Use the sequence periodic ratio, bond measure and maximum periodicity to select patterns
– Based on PFPM and Eclat
PPFP Nofong 2016– Find periodic itemsets using the standard deviation of periods as measure to select patterns.
– Apply a statistical test to select periodic patterns that are significant.
– Vertical algorithm based on Eclat and inspired by OPUS-Miner for the statistical test
PPFP+, PFP+…Nofong 2018 – Find periodic itemsets using the standard deviation and variance of periods as measure to select patterns.
– The measures are integrated in existing algorithms such as PPFP and PFP
PHUSPMDinh 2018– Proposed to find periodic sequential patterns (subsequences that are periodic)
SPP-GrowthFournier-Viger 2019
(ppt)		– Find the stable periodic patterns using a novel measure called lability.
– The goal is to find patterns that are generally stable rather than enforcing a very strict maxPer constraint as many algorithms do.
– Based on FPGrowth
TSPINFournier-Viger 2020– Algorithm for mining the top-k stable periodic patterns.
– Based on SPP-Growth
LPP-Growth
LPP-Miner		Fournier-Viger 2020
(ppt)		– Find locally periodic patterns (periodic in some time intervals rather than the whole database). That is, unlike most algorithms, it is not assumed that a pattern must be always periodic.
– LPP-Growth is based on FPGrowth
– LPP-Miner is based on PFPM, which is inspired by Eclat and Apriori-TID

Implementations

Several algorithms above are implemented in the SPMF data mining software in Java as open-source code.

Some survey papers

I have also written two chapters recently that give some overview of some topics on periodic pattern mining. You may read them if you want to have a quick and easy-to-understand overview of some topics in periodic pattern mining.

Conclusion

In this blog post, I have listed some key references in periodic pattern mining. Of course, I did not list all the references of all authors. I mainly listed the key papers that I have read and found interesting. This is obviously subjective.

Philippe Fournier-Viger is a full professor working in China and founder of the SPMF open source data mining software.

Related posts:

Interview with Prof. Rage Uday Kiran about Data Mining
Happy New Year 2023!
An Overview of Pattern Mining Techniques
Posted in Uncategorized | Tagged , , , , | 4 Comments

Approximate Algorithms for High Utility Itemset Mining

Posted on 2021-05-06 by Philippe Fournier-Viger

On this blog, I have previously given an introduction to a popular data mining task called high utility itemset mining. Put simply, this task aims at finding all the sets of values (items) that have a high importance in a database, where the importance is evaluated using a numeric function. That sounds complicated? But it is not. A simple application is for example to analyze a database of customer transaction to find the sets of products that people buy together and yield a lot of money (values = purchased products, utility = profit). Finding such high utility patterns can then be used to understand the customer behavior and take business decisions. There are also many other applications.

High utility itemset mining is an interesting problem for computer science researchers because it is hard. There are often millions of ways of combining values (items) together in a database. Thus, an efficient algorithm for high utility itemset mining must search to find the solution (the set of high utility itemsets) while ideally avoid exploring all the possibilities.

To efficiently find a solution to a high utility itemset mining problem (task), several efficient algorithms have been designed such as UP-Growth, FHM, HUI-Miner, EFIM, and ULB-Miner. These algorithms are complete algorithms because they guarantee finding the solution (all high utility itemsets) However, these algorithms can still have very long execution times on some databases depending on the size of the data, the algorithm’s parameters, and the characteristics of the data.

For this reason, a research direction in recent years has been to also design some approximate algorithms for high utility itemset mining. These algorithms do not guarantee to find the complete solution but try to be faster. Thus, there is a trade-off between speed and completness of the results. Most approximate algorithms for high utility itemset mining are based on optimization algorithms such as those for particle-swarm optimization, genetic algorithms, the bat algorithm, and bee swarm optimization.

Recently, my team proposed a new paper in that direction to appear in 2021, where we designed two new approximate algorithms, named HUIM-HC and HUIM-SA, respectively based on Hill Climbing and Simulated Annealing. The PDF of the paper is below:

Nawaz, M.S., Fournier-Viger, P., Yun, U., Wu, Y., Song, W. (2021). Mining High Utility Itemsets with Hill Climbing and Simulated Annealing. ACM Transactions on Management Information Systems (to appear)

In that paper, we compare with many state-of-the art approximate algorithms for this problem (HUIF-GA, HUIM-BPSO, HUIM-BA, HUIF-PSO- HUIM-BPSOS and HUIM-GA) and observed that HUIM-HC all algorithms on the tested datasets. For example, see some pictures from some runtime experiments below on 6 datasets:

In this picture, it can be observed that HUIM-SA and HUIM-HC have excellent performance. In a) b) c) d), e), f) HUIM-HC is the fastest, while HUIM-SA is second best on most datasets (except Foodmart).

In another experiment in the paper it is shown that although HUIM-SA is usually much faster than previous algorithms, it can find about the same number of high utility itemsets, while HUIM-HC usually find a bit less.

If you are interested by this research area, there are several possibilities for that. A good starting point to save time is to read the above paper and also you can find the source code of all the above algorithms and datasets in the SPMF data mining library. By using that source code, you do not need to implement these algorithms again and can compare with them. By the way, the source code of HUIM-HC and HUIM-SA will be included in SPMF next week (as I still need to finish the integration).

Hope that this blog post has been interesting! I did not write so much on the blog recently because I have been very busy and some unexpected events occurred. But now I have more free time and I will start again to write more on the blog. If you have any comments or questions, please write a comment below.

—

Philippe Fournier-Viger is a professor of Computer Science and also the founder of the open-source data mining software SPMF, offering more than 120 data mining algorithms.

Related posts:

A Glossary of High Utility Pattern Mining
Test your knowledge about pattern mining!
UDML 2020 – Utility Driven Mining and Learning Workshop
Posted in Pattern Mining, Utility Mining | Tagged , , , , , , , , | 1 Comment

UDML 2021 @ ICDM 2021

Posted on 2021-04-15 by Philippe Fournier-Viger

Hi all, This is to let you know that the UDML workshop on utility driven mining and learning is back again this year at ICDM 2021, for the fourth edition.

UDML 2021 at ICDM 2021 workshop

The topic of this workshop is the concept of utility in data mining and machine learning. This includes various topics such as:

  • Utility pattern mining
  • Game-theoretic multiagent system
  • Utility-based decision-making, planning and negotiation
  • Models for utility optimizations and maximization

All accepted papers will be included in the IEEE ICDM 2021 Workshop proceedings, which are EI indexed. The deadline for submiting papers is the 3rd September 2021.

For more details, this the website of the workshop:
https://www.philippe-fournier-viger.com/utility_mining_workshop_2021/

—

Philippe Fournier-Viger is a full professor working in China and founder of the SPMF open source data mining software.

Related posts:

How to prepare for attending an academic conference?
(video) The EFIM algorithm
We are launching a new data mining journal
Posted in Big data, cfp, Conference, Data Mining, Utility Mining | Tagged , , , , , , , , , | Leave a comment